PSD regulátor se zvukovou kartou [eng]    Nedávno jsem zahlédl na jednom fóru zmínku o regulátoru pro DC motor realizovaném přes zvukovou kartu. To mě docela zaujalo, protože jsem si chtěl už nějakou dobu vyzkoušet diskrétní regulaci na reálném systému, ale nechtělo se mi řešit nějaký komplikovaný analogový vstupně-výstupní interface k PC. Použít k tomuto účelu zvukovou kartu mě skutečně nenapadlo, ale ukázalo se to jako docela použitelné řešení.    Rozhodl jsem se tedy vyzkoušet, na kolik je to použitelné řešení. Původně to měl být jen malý PSD regulátor, ale docela slušně to fungovalo, takže jsem navíc oprášil pár školních projektů a přidal jsem online identifikaci systému a auto-tuning. Jak to chodí si můžete přečíst dále. Varování: Následující text místy předpokládá alespoň základní znalost pojmů z oblasti teorie signálů a systémů a teorie řízení. ;-) Vstupní interface Výstupní interface Časování zvukové karty Struktura programu Něco teorie Testovací program a ovládání Výsledky 1. 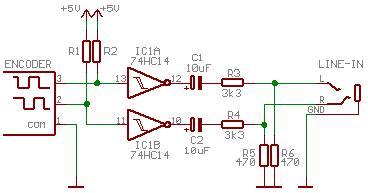Vstupní interface    Základ regulátoru na PC je samozřejmě nějaký vstupní interface pro senzor zpětné vazby. V případě řízení motoru, který jsem si pro ladění vybral, je pro zvukovku nejvhodnější rotační enkodér. Kvadraturní signál enkodéru lze po vhodné úpravě úrovní připojit přímo k line-in vstupu zvukovky:    Nejedná se o nic jiného, než tvarvač signálu a úpravu amplitudy na cca 700mV, což je u mé zvukovky asi tak 70% fullscale signálu. 2. 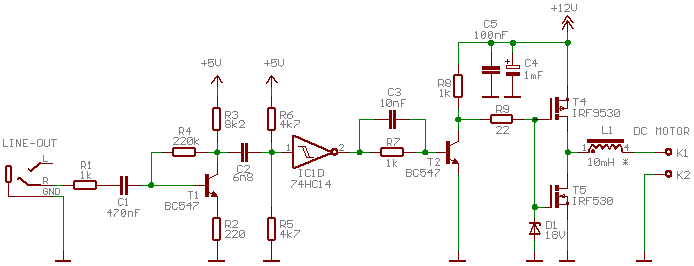Výstupní interface    Druhou nezbytnou součástí je výstupní interface pro regulovaný systém. V mém případě jsem se rozhodl ladit algoritmus na malém DC motorku s PWM regulací. Ze stolních sedimentů jsem sestavil následující tvarovač a výkonový stupěň:    Použité řešení není zrovna optimální, ale vhodnější komponenty nebyly po ruce. :-) Konkrétní hodnoty součástek vychází z toho, co bylo zrovna na stole. Zapojení docela uspokojivě fungovalo v rozsahu 100Hz až 1kHz, což je pro malé DC motorky asi tak optimum (laděno na 480Hz). Princip funkce je jednoduchý: Zesílit signál zvukovky a derivačním členem C2, R5||R6 vytvořit zapínací a vypínací impulzy pro schmittův KO. Na výstupu IC1 by už měl být čistý PWM signál. Drobný problém je, že při výpadku PWM signálu může KO zůstat viset v libovolném stavu. Z toho důvodu je výstupní střída z PC omezena tak, aby vždy minimálně jeden vzorek na periodu měl opačnou hodnotu, tj. střída nikdy není 0 ani plných 100%.    "Výkonová" část je určena pro malé DC motorky s napětím do cca 15V. Při vyšším napětí nelze toto řešení použit, protože by to neunesly gaty MOSFETů. Zenerka je tam jen pro jistotu, kdyby přes kapacitu DG prolezly nějaké špičky od indukční zátěže. Tlumivka na výstupu sice nutně být nemusí, ale motoru rozhodně prospěje (vyhlazuje proud). Jeden motorek bez tlumivky jsem během nešetrných experimentů s regulátorem a nízkou frekvencí PWM totélně zničil (kluzná ložiska toho moc nevydrží). :-( Konkrétní hodnota tlumivky záleží na motoru.    Uvedené zapojení umožňuje řídit otácky pouze v jednom směru. Pro obousměrný provoz by bylo potřeba použít plný můstek. 3. 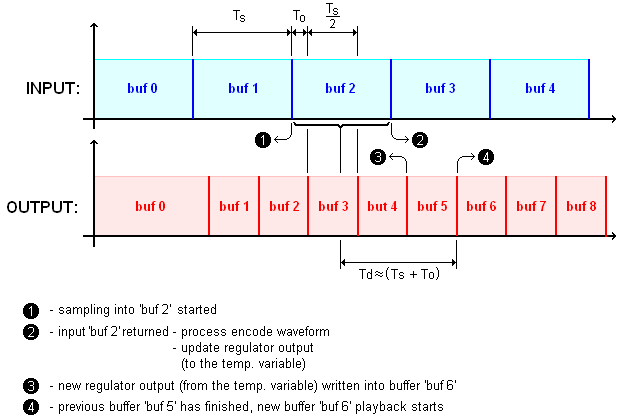Časování vstupu a výstupu zvukové karty    Docela zásadní problém při řešení real-time řízení je vyřešit správně časování. Je zjevné, že od začátku vzorkování výstupu enkodéru (1) až ke skutečné změně výstupního signálu zvukovky (4) uplyne docela dost času. Grafické znázornění časování je na následujícím obrázku:    Přinejmenším je třeba vzít v úvahu, že zpracováním právě navzorkovaného úseku z enkodéru se získá průměrná hodnota za celý interval (1) až (2), tj. dopravní zpoždění cca Ts/2. Dále se musí počítat s tím, že výstup musí být minimálně dvojitě bufferovaný (střídavě se do jednoho bufferu zapisuje a z druhého se přehrává), takže než se nově naplněný buffer v okamžiku (3) dostane na DAC zvukovky (4) uplynulo by dalších Ts. Kvůli zkrácení tohoto zpoždění jsem zvolil délku výstupních bufferů na jednu polovinu vstupních, takže i toto zpoždění dělá Ts/2.    Poslední nutností je časově posunout výstupní intervaly proti vstupním, protože výpočet výstupu regulátoru, případně další operace, pochopitelně nějakou dobu trvají a musí se dokončit, než si zvukovka/systém vyžádá naplnění dalšího výstupního bufferu (3). Kvůli tomu je nutné přidat další zpoždění To (reálně asi 20ms). Celkové dopravní zpoždění přidané k vlastnímu regulovanému systému tedy dělá cca (Ts + To), což je minimálně asi 80ms. Při kratších bufferech už docházelo k podtečení.    Zpoždění by se jistě dalo zkrátit tak, že by se přepisoval obsah výstupního bufferu i když už je přiřazen zvukovce a přehrává se z něj, ale nepřišlo mi to zrovna jako čisté řešení. 4. 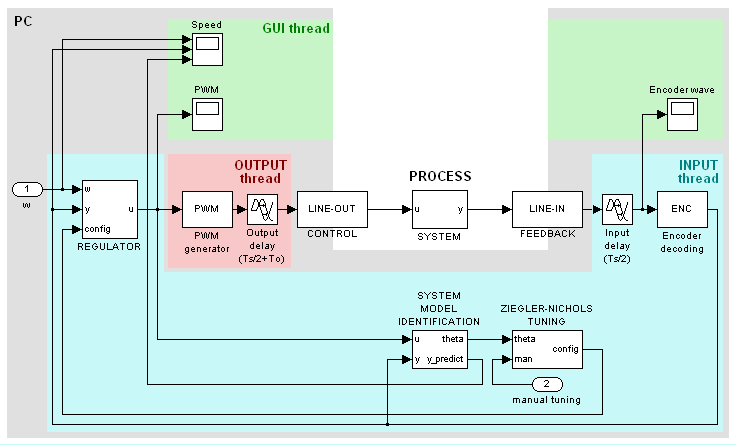Struktura programu    Blokovou strukturu celého prográmku ukazuje následující diagram:    Aby bylo dodržené časování audio vstupu i výstupu, je program rozdělen na tři vlákna. Hlavním vláknem je uživatelské rozhraní v Borland VCL. Tím jsou ovládány všechny ostatní moduly programu.    Obsluha audio vstupu je řešena samostatným vláknem a provádí se v něm také všechny výpočty, protože jsou všechny vázané na nová vstupní data.    Výstupní vlákno pouze generuje PWM průběh podle akčního zásahu vypočteného ve vstupním vlákně a aby nedocházelo k podtečení audio výstupu, když probíhají časově náročné operace (identifikace, vykreslování grafů, ...) má zvýšenou prioritu. Mělo by to takto fungovat skoro jako přerušení na jednočipu. Díky tomu by měla aplikace chodit i na pomalých jednojádrových strojích (zkoušel jsem to na P3 1GHz a zdálo se to být funkční). 5. Něco teorie    Následujících pár odstavců je zjednodušená teorie, popisující algoritmy a matematiku použitou pro jednotlivé funkce testovacího programu. 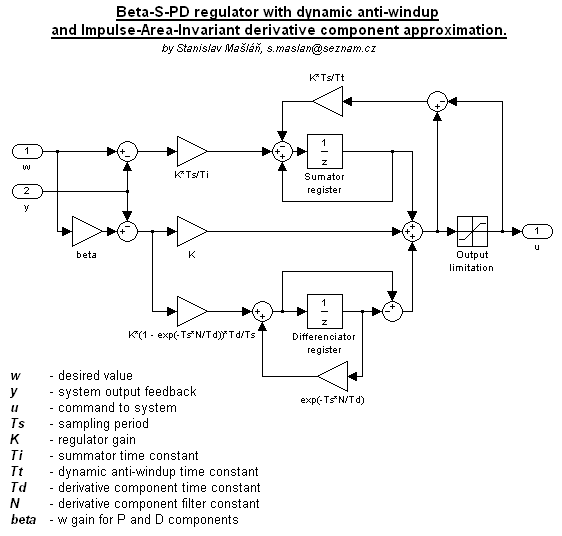5.1 Regulátor    Původní záměr byl zkusit jen obyčejný PSD regulátor (číslicová obdoba PID), ale docela pěkně to fungovalo, takže jsem nakonec implementoval tzv. beta-S-PD topologii s dynamickým omezením integrační složky, která umožňuje podstatně lépe tvarovat odezvu uzavřené smyčky. Blokové znázornění topologie ukazuje následující schéma:    Derivační složka je samozřejmě filtrovaná, nefiltrovanou nemá cenu používat, protože obvykle nadělá více škody, než užitku. S pomalým vzorkováním je její amplituda malá a téměř se neuplatní, s rychlým by musela být pro dosažení stejné energie obrovská a takové jehlové pulzy zrovna nesvědčí mechanické části systému. Navíc by výrazně zesílila šum. Proto je vždy rozumné použít filtrovanou verzi, která impulz "protáhne" v čase. Pro její diskrétní aproximaci je zde použita metoda Impulse-Area-Invariant. Tuto celkem novou metodu vyvinuli před pár lety na VUT Brno (FEKT, ÚAMT) a pokud je mi známo, tak se jedná o jediný přímý ekvivalent spojité filtrované derivace. Korekční koeficient amplitudy je zde vypočten tak, aby derivátor dodal systému energii identickou jako spojitá verze bez ohledu na vzorkovací periodu. Díky této příjemné vlastnosti lze pro návrh regulátoru použít stejné metody jako pro spojitý PID regulátor.    Omezení integrační složky (anti-windup) je zde řešeno dynamicky s časovou konstantou Tt. Sice je to další parametr navíc, který je třeba nastavit, ale zase to umožňuje ovlivnit tvar odezvy uzavřené smyčky. Prostou limitaci sumátoru v topologii beta-S-PD použít ani nelze, protože by pro malé beta nešlo dosáhnout plný akční zásah.    Význam parametru beta spočívá v omezení citlivosti složek P a D na vstup žádané hodnoty w. S-složky se kvůli dosažení nulové ustálené regulační odchylky parametr netýká (proto se topologie značí S-PD). Pro beta=1 se jedná o klasický PSD, pro beta=0 pak S-PD. Volbou hodnoty beta někde mezi 0 a 1 lze nastavit vhodný tvar odezvy uzavřené smyčky na řízení (např. omezit překmit), ale odezva na poruchu zůstává neměnná. Jedná se tedy o jednodušší variantu regulátoru s více stupni volnosti. Něco k metodě Impulse-Area-Invariant lze najít třeba zde: PIVOŇKA, Petr., SCHMIDT, Michal. Comparative Analysis of Discrete Derivative Implementations in PID Controllers. 2007. Brno University Of Technology, Department of Control and Instrumentation, Kolejní 2906/4, CZECH REPUBLIC. 5.2 Online identifikace systému    Po odladění vlastního audio vstupu, výstupu a regulátoru jsem si řekl, že by nebylo od věci přidat online identifikaci procesu (regulovaného systému) s automatickým nastavováním regulátoru. Metod online identifikace je celá řada. Nejrozšířenější je zřejmě runtime varianta metody nejmenších čtverců, ale do toho se mi moc nechtělo, takže jsem raději zrecykloval jeden svůj starší školní projekt, kde jsem měl implementovaný neuronový ARX model třetího řádu s minimalizační metodou Steepest-Descent (déle SD). Zní to možná trochu složitě, ale ve skutečnosti je to jedna z nejsnažších metod.    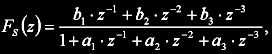Hledaný z-přenos procesu Fs(z) má tvar: kde koeficienty a1,2,3 až b1,2,3 jsou hledané paramtery systému. Třetí řád je sice pro motor zbytečně mnoho, ale na druhou stranu je třeba počítat s uvedeným dopravním zpožděním, které "spotřebuje" celý jeden člen z čitatele (b1) a výpočetní nároky nejsou na dnešních PC podstatné. 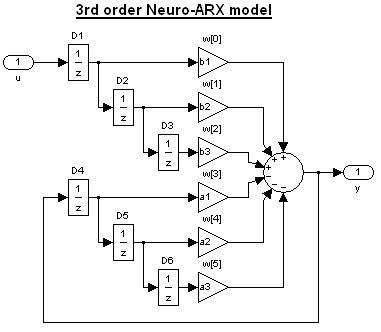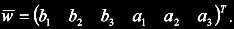Realizace toho systému neuronovým modelem je následující:    Vektor vstupních vah neuronu w obsahuje jednotlivé koeficienty hledaného systému v pořadí:    Vlastní algoritmus SD potřebuje ke své funkci jen dvě věci: Matici předloh X s n vzory (zpožděné vstupy a výstupy procesu) a vektor pozorování t (požadované výstupy modelu). 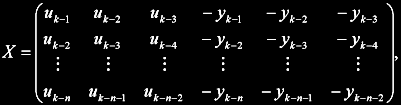Matice X obsahuje vždy zpožděné vstupy u a výstupy y procesu podle vzoru: kde u-k resp. y-k jsou vstupní resp. výstupní vzorky z procesu zpožděné o k period. Jednotlivé řádky matice zde odpovídají jednotlivým vzorům, na které je neuron učen (každý rádek odpovídá jedné vzorkovací periodě). 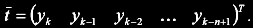Vektor pozorování t obsahuje opět výstupy procesu, ale tentokrát bez zpoždění prvního vzorku:    Vlastní minimalizační algoritmus SD s tzv. optimálním krokem ε je celkem jednoduchý:    Celý algoritmus obsahuje pouze základní maticové operace, inverze při výpočtu optimálního kroku ε je pouze skalární, takže není třeba řešit docela problematickou inverzi matice. K ukončení procesu učení dojde při poklesu chyby modelu err pod nastavený práh nebo při překročení maximálního počtu iterací.    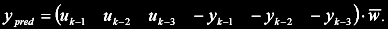Pro jednokrokovou predikci výstupu modelu platí:    Celý SD algoritmus je díky použití optimálního kroku ε poměrně snadný na nastavení. Je třeba pouze rozumně zvolit počet vzorů n, tj. jak daleko nazpět v čase algoritmus "vidí". Minimální délka je omezená řádem systému s stabilitou identifikovaných parametrů na minimálně asi 20 vzorků, maximální délka je zase omezená výpočetní náročností asi na 1000 vzorků.    Dále je třeba nastavit ukončovací podmínky procesu učení, tj. maximální chybu modelu a limit počtu iterací, protože ne se všemi vstupními daty lze identifikaci provést. Nastavení těchto parametrů hodně závisí na charakteru procesu. Cílová chyba by měla být nastavena tak, aby po nějakém čase byla dosažena - aby algoritmus neustále nedobíhal až do maximálního počtu iterací. Může se totiž snadno stát, že se model přeučí (naučí se i šum ve zdrojových datech). Něco málo informací k SD metodě (mimo jiné) je k dispozici třeba zde: LEBEDA, Aleš. Model soustavy motorů s pružným členem: diplomová práce. Brno: Vysoké učení technické v Brně, Fakulta elektrotechniky a komunikačních technologií, Ústav automatizace a měřicí techniky, 2012. 80 s. Vedoucí práce byl prof. Ing. Petr Pivoňka, CSc. 5.3 Auto-tuning    Když už jsem odladil identifikaci, přidal jsem také funkci pro automatické nastavování regulátoru. Metod je opět celá řada, ale zřejmě nejjednodušší je starý známý Ziegler-Nichols. K tomu je nejprve třeba vypočítat kritické parametry, tj. kritické zesílení uzavřené smyčky Kk a odpovídající periodu oscilací Tk. Pomocí těchto parametrů se pak nastavují parametry PSD: K = 0.6*Kk Ti = 0.5*Tk Td = 0.125*Tk Alternativní varianta s potlačením kmitavé odezvy: K = 0.3*Kk Ti = 1.0*Tk Td = 0.125*Tk    Výpočet kritických parametrů pro systém třetího řádu je poměrně zdlouhavý. 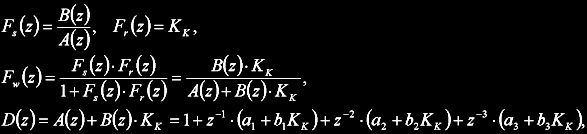Vychází se z charakteristického polynomu uzavřené smyčky s P regulátorem: kde Fw je přenos uzavřené smyčky, Fs přenos procesu, Fr přenos regulátoru a Kk hledané kritické zesílení. Charakteristický polynom D obsahuje tři póly. Systém se může dostat na mez stability a zároveň kmitat jen ve dvou případech.    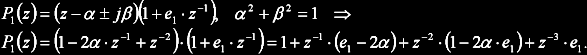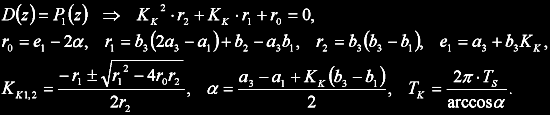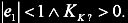První varianta nastane, když komplexní pár pólů leží na jednotkové kružnici a zbývající pól je stabilní (uvnitř jednotkové kružnice):    Dosazením P1 do rovnosti charakteristickému polynomu uzavřené smyčky D lze získat dvě řešení pro kritické zesílení a periodu kmitů:    Jedno z řešení je použitelné pokud jsou splněny podmínky:    Pokud ani jedno řešení není platné, může nastat ještě druhá varianta: jeden reálný záporný pól na jednotkové kružnici (z = -1) a zbývající dva stabilní. 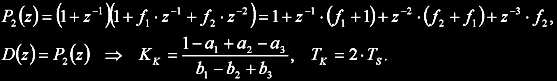Dosazením P2 do rovnosti charakteristickému polynomu uzavřené smyčky D lze získat následující řešení:    Kritická perioda je v tomto případě dána jen periodou vzorkování. 6. Testovací program a ovládání    Prográmek je jako obvykle napsán v BDS2006 Turbo C++ a testován ve Windows XP. Odladěn byl tentokrát na Intel Core i5 (4-jádro) a zdál se být funkční i na stařičkém P3 1GHz. Fungovat by měl i ve Windows 7 (API pro zvukovku se snad neměnily). S optimalizací jsem se nijak zvlášť neobtěžoval, takže grafy jsou celkem náročné (částečně používají velmi pomalou třídu TCanvas) a online identifikace nevyužívá pro maticové operace žádné speciální instrukční sady, takže pro vyšší počet iterací si také o nějaký ten výkon řekne.    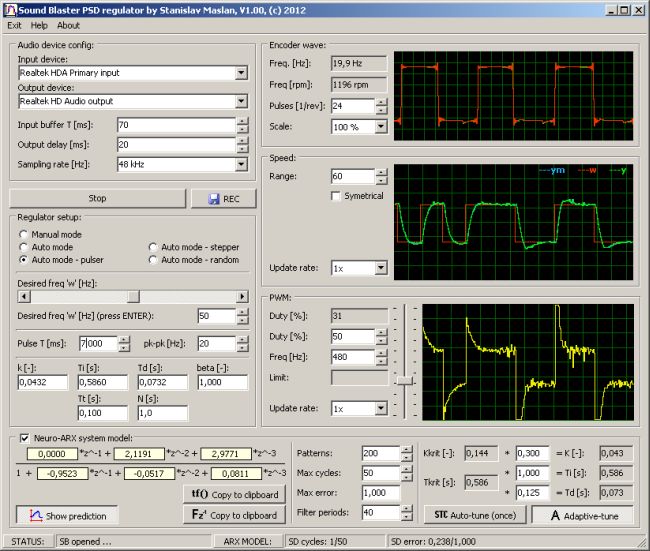Prográmek je částečně poskládaný ze zdrojáků, které jsem psal už dříve, tkaže je poněkud nekonzistentní, ale zase jsem dost komentoval, takže by neměl být problém se v tom vyznat. Kromě hlavního modulu (GUI) je všechno ostatní napsáno jen pomocí standardních knihoven C/C++ a WinApi (windows.h, mmsystem.h), takže by neměl být problém použít moduly s jiným GUI. Program a zdrojáky V1.00, 10.10.2012 ke stažení: SB_regulator.zip (980kB). 6.1 Licence    Zdrojový kód může být použit v libovolném projektu, ale byl napsán čistě pro studijní účely, takže autor nenese zodpovědnost za jeho funčnost a za případné škody vzniklé jeho použitím. 6.2 Nastavení zvukovky    Zvukovku je třeba nastavit externě pomocí ovladačů tak, aby měl výstup maximální hlasitost a v možnostech záznamu vstup z LINE-IN. Citlivost vstupu bude s uvedenými hodnotami součástek patrně na maximum, vhodnou hodnotu lze určit z oscilogramu enkodéru.    V programu je předně třeba vybrat odpovídající vstupní a výstupní zařízení. Pokud to má fungovat, musí pochopitelně patřit vstupní i výstupní zařízení stejné zvukové kartě, jinak by se rozjela synchronizace a nebylo by splněné časování podle bodu 3.    Vzorkovací periodu je třeba nastavit podle chování procesu. Nejmenší hodnota, při které ještě nedocházelo k podtékání bufferu, byla v mém případě 70ms (výstupní buffer je poloviční, takže už je to dost na hraně). Pokud je nastavena příliš krátká perioda, bude výstupní tón přerušovaný.    Dále je třeba nstavit časový posuv výstupu proti vstupu. Fungovat by to mělo při nastavení na 20ms, ale lze ho lehce měnit. Nesmí ale být vyšší, než půl vzorkovací periody.    Vzorkovací kmitočet lze sice měnit, ale není valný důvod volit nižší, než 48kHz - ani to není pro velké otáčky dostatečné. 6.3 Nastavení enkodéru    U grafu enkodéru lze nastavit jen počet impulzů na otáčku. Enkodér je automaticky vyhodnocován jako kvadraturní (detekce směru otáčení), takže pokud je použita jen jednoduchá optozávora, měl by být její signál přiveden na oba vstupy LINE-IN! Pokud je k řízení motoru použit plný můstek (obousměrný pohon), pak je třeba u grafu "Speed" zaškrtnout možnost "Bidirect". Ta vloží do PWM výstupu offset 50%, tj. pro nulový proud motorem bude střída 50%. 6.4 Nastavení PWM    Vedle grafu PWM je možné nastavit kmitočet PWM. Rozumné hodnoty jsou tak 100Hz až 1kHz. Pro nižší by bylo třeba vyhlazovat proud motoru velkou indukčností a pro vyšší už nedostačuje vzorkovací kmitočet (zvyšuje se výstupní šum). 6.5 Nastavení regulátoru    Zde lze předně vybrat režim funkce. Jednak je k dispozici manuál, kdy se ovládá přímo střída PWM (trackbar u grafu), dále pak automat (regulátor) nebo automat s automatickým generátorem akčního zásahu (hodí se pro identifikaci a ladění).    V automatickém režimu se uplatní pole pro nastavení parametrů regulátoru. Jejich význam je uveden v popisu topologie regulátoru (5.1). Jediný z parametrů, kterů by mohl dělat problémy je časová konstanta anti-windup Tt. Když je její hodnota moc vysoká, nedojde k omezení integrační složky a když příliš nízká může dojít k oscilacím, takže je dobré tento parametr postupně snižovat, dokud se viditelně nezmění odezva regulátoru. Pochopitelně se uplatní jen, když akční zásah (střída PWM) dosahuje limitace. 6.6 ARX model + Auto-tuning    V této sekci lze nastavovat parametry identifikačního algoritmu (viz popis algoritmu 5.2) a dále pak lze provést jednorázové nastavení PSD nebo zapnout adaptivní režim (kontinuální dolaďování). Kritické parametry jsou zde pronásobeny nastavitelnými koeficienty podle metody Ziegler-Nichols (5.3), pak je jimi přepsáno nastavení regulátoru. Ovlivňovány jsou pouze parametry K, Ti a Td, ostatní je třeba nastavit ručně.    Aby algoritmus správně pracoval, musí se pochopitelně se sytémem něco dít. Není možné identifikovat parametry v ustáleném stavu. K tomu je ideální použít generátor impulzů nebo šumu. Automatické nastavení regulátoru má pochopitelně smysl jen, když jsou již ustálené parametry modelu, resp. kritické parametry.    Model je možné exportovat v textovém režimu ve formátu použitelném pro Matlab nebo Octave (alespoň doufám, že je to kompatibilní). 6.7 Kritické póly uzavřené smyčky    Přes menu "View" lze zobrazit graf s rozložením pólů uzavřené smyčky při kritickém zesílení. Tento graf se může docela hodit při určení vzorkovací periody. Je vhodné, aby na jednotkové kružnici (mez stability) ležel kmitavý pár pólů, nikoliv zbývající reálný. Pak se totiž metodě Zigler-Nichols zdrovna moc nedaří. 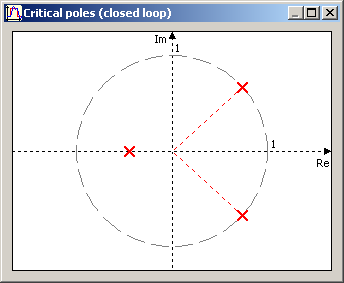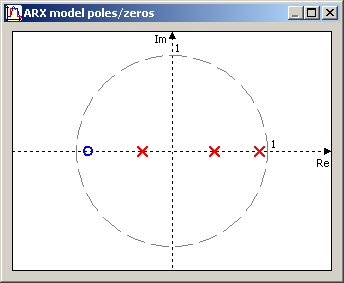6.8 Póly a nuly ARX modelu    Přes menu "View" lze zobrazit zobrazit graf s rozložením pólů a nul ARX modelu. Hodí se ke grafickému znázornění pohybu kořenů čitatele a jmenovatele modelu v průběhu identifikace. Je zde použit celkem komplikovaný výpočet kořenů kubické rovnice, takže si nejsem zdela jist, jestli to vždy počítá správně, ale alespoň pro pár základních rovnic výsledky odpovídaly. 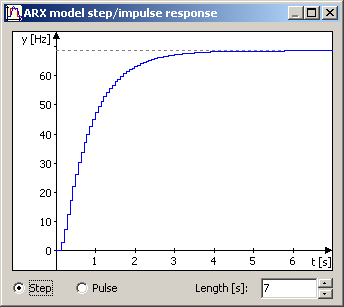6.9 Odezva na jednotkový skok/impuls    Přes menu "View" lze zobrazit zobrazit odezvu ARX modelu na jednotkový skok nebo impulz. Algoritmus vykreslování os není zrovna vyladěn, takže těžko říct, co to bude dělat třeba pro bipolární průběhy, ale zdálo se to být celkem funkční. 6.10 Ostatní    Dvojklik na kterýkoliv z grafů nabídne možnost exportu 24-bit BMP obrázku. Při stisknutém tlačítku "REC" je vytvořen/přepsán soubor "rec.csv" ve složce programu a začnou se do něj ukládat hodnoty z grafů. Formát je standardní CSV oddělovaný středníkem. 7. Výsledky    K testování programu jsem si vybral malý DC motorek. Nemá žádné dohledatelné označení a asi to ani není motor. Podle konstrukce je to pravděpodobně tachodynamo - má mnohapólové samonosné vinutí ve vzduchové mezeře magnetu (zádné jádro) a nijak se nezahřívá ani při 30V. Na hřídel jsem přidal malý setrvačník pro zvýšení dynamiky. Pro zpětnou vazbu jsem použil nějakou reflexní optozávoru z videa s 24 pulzy na otáčku.    Systém má poměrně rychlou odezvu (dominantní časová konstanta cca 800ms), takže jsem nastavil vzorkování na maximum (70ms). Vzorkovací kmitočet jsem kvůli šumu nastavil na maximum (96kHz).    Pro snažší identifikaci jsem použil automatický generátor skoků řízení s periodou 8s a pk-pk amplitudou 25Hz (1500ot/s). Model se chytil a celkem ustálil během asi 7s. 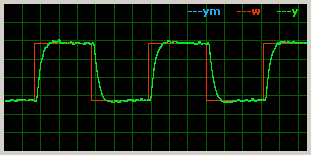Koeficienty pro ZN metodu jsem nastavil na variantu pro potlačení kmitavé odezvy. 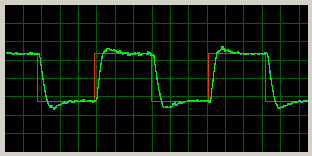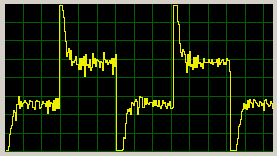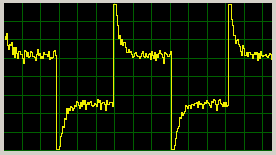Po doladění anti-windup konstanty Tt, filtru derivace N a koeficientu beta jsem dostal celkem pěknou odezvu na skok řízení:    Akční zásah je sice trochu zašuměný, ale to je způsobeno zpětnou vazbou. S vyšší dynamikou motoru se to neprojeví, ale asi by to chtělo nějakou lepší metodu vyhodnocovaní otáček (momentálně používám počítání pulzů a jejich celkové délky).    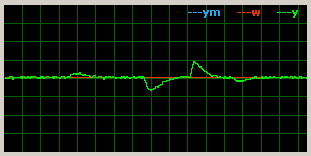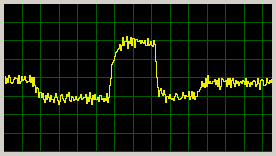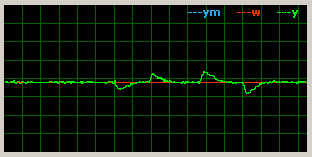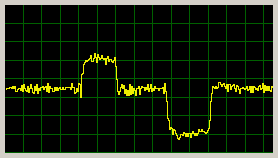Odezva na skok poruchy (multiplikativní - změna napájecího napětí 12-16-7-16-12V) pak vypadala při stejný parametrech takto:    Reakce na aditivní chybu na vstupu systému (odečtení/přistění malého proudu k PWM výstupu):    Takže na závěr: Použití zvukovky jako vstupně/výstupního rozhraní k regulaci zřejmě možné je, ale dobře to bude fungovat jen za přepokladu větší dynamiky systému. Použitý přístup neumožňuje zkrátit dopravní zpoždění pod cca 80ms. (c) 2012, Stanislav Mašláň - Všechna práva vyhrazena. Last update: 10.10.2012