
Před pár týdny jsem řešil jednoduchý impulzní zdroj přímo řízený PWM výstupem jednočipu AVR. Součástí byla zpětná vazba proudu přes měřící trafo a vzhledem k chlupatému průběhu proudu to chtělo true-RMS detektor. Původně jsem zvažoval nějaký analogový detektor, ale pak jsem si řekl proč to komplikovat? Proč to nezkusit digitálně přímým vzorkováním průběhu ADC převodníkem v AVR? Signál měl sice 40 kHz, zatímco převodník má pro plné rozlišení vzorkování jen 15 kS/s, ale signál je periodický, navíc generovaný přímo AVRkem, takže se přímo nabízelo použít tzv. vzorkování v ekvivalentním čase (Equivalent Time Sampling - ETS), kterým lze vzorkovat průběhy s mnohonásobně vyšším kmitočtem, než udává Nyquistův vzorkovací teorém pro vzorkování v reálném čase. Jediná otázka zní, jaká je skutečná analogová šířka pásma ADC převodníku AVRka? ATMEL ji bohužel v datasheetu nedefinuje. Následující text se tedy zabývá realizací ETS vzorkování a měřením analogové šířky pásma ADC převodníku.
Jak jsem zmínil ETS jsou všeobecně techniky, které umožňují u stabilních a periodických signálů vzorkovat průběhy s frekvenčními složkami přesahujícími
Nyquistovo vzorkovací kriterium (fs/2). Tyto techniky byly hodně populární a často také jediné možné řešení u starých vzorkovacích osciloskopů (DSO), protože rychlé ADC
převodníky nebyly nebo se vyráběly za astronomické částky pro high-end přístroje a to se ještě muselo vzorkování rozložit na N dílčích převodníků s rozfázovanými hodinami.
To se ostatně dělá z cenových důvodů do dnes, viz třeba Rigol DS1052 s 5ti převodníky AD9288 (mimochodem údaně přetaktovanými ze 40 na 100 MHz - ani vybrušování potisku čipu jim nepomohlo to zakrýt :-).
Dnes se skládané vzorkování používá většinou už jen v hračkách jako PicoScope nebo naopak u extrémně rychlých DSO, kde to prostě v reálném čase nejde.
Konkrétních realizací je několik, jedná se buďto o sekvenční vzorkování nebo náhodné vzorkování a jejich různé realizace. Nebudu popisovat jednotlivé metody, protože je toho
plný internet (i česky), zaměřím se pouze na speciální případ snadno realizovatelný v mém případě. Jde o sekvenční vzorkování bez synchronizace.
Celá myšlenka je založená na tom, že při určitém konkrétním poměru vzorkovacího kmitočtu a měřeného kmitočtu dojde ke vzniku tzv. aliasu s určitým časovým měřítkem, pořadím vzorků a s
celočíselným počtem vzorků na periodu signálu. Díky tomu bude alias při kontinuálním vzorkování statický (nebude "ujíždět" stranou jako na osciloskopu bez synchronizace).
Příklad takové situace je na obr 1.1.
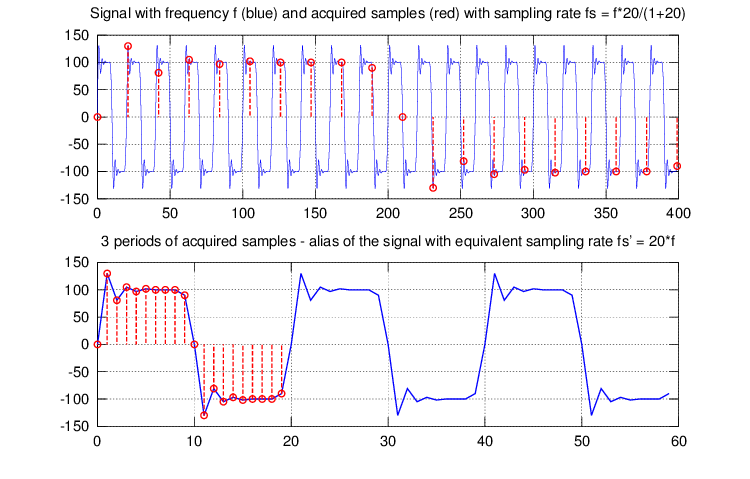 Obr. 1.1 - Příklad sekvenčního vzorkování v ekvivalentním čase.
|
Horní graf ukazuje originální průběh s kmitočtem f a vzorkovací intervaly s kmitočtem fs. Poměr obou kmitočtů je zde nastaven přesně na r = 20/(1+20), takže každý další vzorek
je proti začátku periody signálu zpožděn o 1/20 periody T více, než předchozí. Po navzorkování 20ti vzorků je zase zpoždění vzorku proti začátku periody signálu nulové a je tedy navzorkována jedna plná perioda průběhu.
Spodní graf pak ukazuje průběh zrekonstruovaný z těchto 20ti vzorků. Zvětšení v časové ose je 20x, ekvivaletní vzorkovací kmitočet je 20*f, tj. (20+1) krát vyšší, než skutečný vzorkovací kmitočet fs.
Poměr r byl zvolen tak, aby vzorky měly správné pořadí a nebylo je tudíž třeba nijak přeskládávat v paměti a navíc zvolený poměr zajišťuje, celočíselný počet vzorků na periodu T,
takže odpadá potřeba synchronizace.
Toto byl samozřejmě ideální případ, který v praxi moc reálný není, protože zajistit přesný poměr r v případě, že měřený průběh pochází z jiného zdroje dost dobře nelze, resp. je to
celkem složité. Rozlišení časovačů nebo PLL pro generování vzorkovacího kmitočtu je omezené, takže pro generování přesného vzorkovacího kmitočtu zbývá buďto použít důkladně filtrovaný DDS generátor nebo
použít alternativní přístup: Změření kmitočtu měřeného signálu, volba vhodného vzorkovacího kmitočtu dle dostupných možností a následné přeskládání
vzorků dle jejich skutečné pozice v periodě signálu. Jednoduchý příklad: Je nastaveno takové vzorkování, že poměr kmitočtů 1/r = 2.71. Tj. každý další vzorek je zpožděn o 2 celé periody signálu a 0.71*T proti předchozímu.
Integrací 1/r lze pak snadno spočítat polohu každého vzorku v rámci periody signálu. Příklad je uveden v tab. 1.1.
| vzorek | relativní čas | relativní pozice vzorku |
|---|---|---|
| 0 | 0.00*T | 0.00*T |
| 1 | 2.71*T | 0.71*T |
| 2 | 5.42*T | 0.42*T |
| 3 | 8.13*T | 0.13*T |
| 4 | 10.84*T | 0.84*T |
| 5 | 13.55*T | 0.55*T |
| 6 | 16.26*T | 0.26*T |
| 7 | 18.97*T | 0.97*T |
| ... | ... | ... |
Tab. 1.1 - Přeskládání vzorků při vzorkování v ekvivalentním čase. |
Poslední sloupec (desetinná část relativního času) udává relativní pozici vzorku v rámci periody vzorkovaného signálu. Na základě tohoto parametru pak lze vzorky přeskládat (vybrat si) tak, abych dostal rekonstruovaný signál v požadovaném měřítku. Např. pokud budu chtít rekonstruovat signál s časovým zvětšením 5x, tak budu postupně hledat vzorky se zpožděním nejbližším hodnotám 0.00T, 0.20T, 0.40T, 0.60T a 0.80T. Je celkem zřejmé, že čím větší zvětšetní budu potřebovat, tím více vzorků musím nabrat a samozřejmě musím zvolit r, které není blízko celému číslo nebo nějakému nevhodnému racionálnímu číslu. V opačném případě budou v navzorkovaném průběhu vzorky s některými zpožděními chybět a rekonstruovaná perioda bude "děravá". Konkrétní realizace této metody je ukázána na obr 1.2.
 Fig. 1.2 - Experimentální DSO se vzorkováním v ekvivalentním čase.
|
Průbeh na obrázku je screenshot z mého postaršího experimentálního DSO. Reálný vzorkovací kmitočet byl 32 MS/s, paměť měla jen 4 kS, ale i tak bylo možné dosáhnout časového zvětšení 50x a chybělo zpravidla jen nekolik vzorků (to jsou ty zuby v průběhu). Ekvivalentní vzorkování bylo v tomto případě 1.6 GS/s. Bohužel HW onoho DSO nebyl pro tuto metodu navržen a neumožňoval nastavit vzorkovací kmitočet, takže tento trik fungoval jen pro některé kmitočty. Pokud došlo k nevhodnému poměru r, tak to dopadlo jako na obr 1.3.
 Fig. 1.3 - Experimentální DSO se vzorkováním v ekvivalentním čase - nevhodný poměr r.
|
I když poměr r nebyl přesně x.0000, byl tomu hodně blízko, takže 4 kS paměť prostě nestačila a průběh je děravý. Dala by se sice použít interpolace, ale ta by pouze vyhladila průběh, žádné detaily vykouzlit nedovede.
Naštěstí v případě mého impulzního zdroje je jak měřený průběh, tak ADC taktován ze společného zdroje hodin a i s omezeným rozlišením časovačů AVR lze
najít taková nastavení, kdy vznikne žádaný statický alias s dostatečným počtem vzorků na periodu signálu. Sice často se vzorky ve změněném pořadí, ale přeskládávání je tak snadné,
že ho lze snadno provádět v reálněm čase přímo při vzorkování.
Protože hledat metodou pokus omyl není zrovna optimální, napsal jsem pro tento účel jednoduchý skript pro GNU Octave/Matlab.
Po nastavení pár parametrů, jako kmitočet hodin, ADC a rozsahu generovaných kmitočtů na PWM kanálu vysype možná nastavení timeru PWM kanálu, pro keteré bude výsledkem
statický alias. Dále také vypisuje organizaci dat, protože pro některá nastavení je alias složen z nekolika sekvencí vzorků, které je třeba proložit. Tedy pouze v případě, že
je třeba průběh zobrazit - u výpočtu true-RMS na pořadí vzorků nezáleží.
GNU Octave skript pro nastavení AVR pro ETS vzorkování: Octave_AVR_ets.zip (10 kB).
Po odladění samotného vzorkování jsem se rozhodl zjistit, jak je to s onou šířkou pásma ADC. ATMEL uvádí 38.5 kHz, což je evidentně Nyquistova frekvence pro nejrychlejší takt ADC a to samozřejmě nemá s analogovou šířkou pásma co dělat. Ta je daná následujícími parametry:
- Sériová vstupní impedance Z (interní+externí).
- Kapacita kondenzátoru Ch v Sample & Hold obvodu.
- Doba vzorkování tsh S&H obvodu.
V jiné části datasheetu je uvedeno zjednodušené náhradní schéma ADC. Dlě něj je kapacita Ch cca 14 pF.
Sériový odpor R pak něco mezi 1 a 100 kOhm. To by znamenalo útlum o 3 dB v rozsahu:
f0 = 1/(2*pi*R*C) = 114 kHz až 11.4 MHz.
To mi zrovna moc nepomohlo. Parametr 3) je ještě nejistější. Z grafu je sice vidět, kdy je vzorkování skončeno (1.5 cyklu po začátku převodu pro free-running režim), ale ne kde začíná.
Pokud by vzorkování trvalo celých 1.5 cyklu, tak by to odpovídalo intervalu 7.5 µs pro maximální takt ADC 200 kHz. Ideální by bylo, kdyby
vzorkování trvalo násobně déle, než je časová konstanta R*Ch, protože pak se na šířce pásma nijak neprojeví (dominantní vliv bude mít časová konstanta R*Ch).
Naopak pokud by byl interval tsh srovnatelný nebo kratší, tak omezuje nabíjení kapacity Ch a dojde k dalšímu poklesu
šířky pásma. Čili trochu paradoxně dosáhnu lepší šířku pásma s pomalejším taktem ADC, tj. delším intervalem tsh. :-)
Vzhledem k nedefinovaným parametrům je tedy nutné šířku pásma změřit. K tomu účelu jsem zvolil
metodu porovnání spekter: Na vstup ADC je přiveden signál se známým spektrem, průběh je navzorkován a jeho spektrum porovnáno s referenčním spektrem získaným z DSO vzorkujícího přímo na vstupu ADC.
Poměr obou spekter je přímo frekvenční přenos analogové části ADC. Jako optimální průběh se zde hodí obdélník,
protože obsahuje dostatek harmonických složek, které lze porovnat.
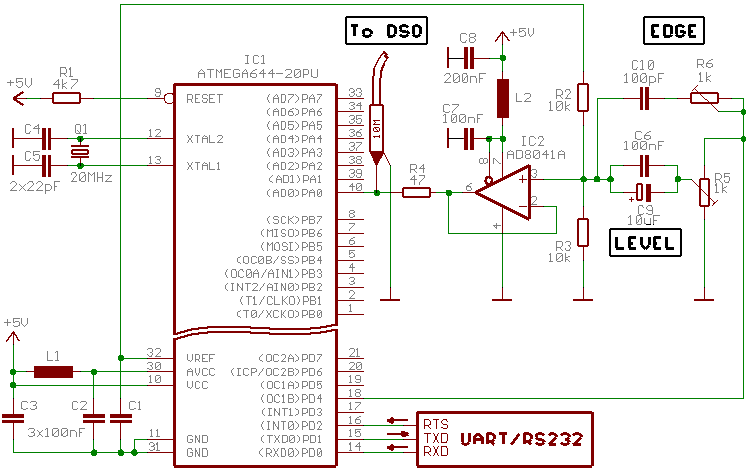 Fig. 2.1 - Schéma zapojení pro měření šířky pásma AVR ADC.
|
Schéma zapojení experimentu je na obr. 2.1. AVRko generuje obdélník se střídou cca 50 % na výstupu OC1B.
Signál je veden do rail-to-rail operáku AD8041 (náhodou byl zrovna zapíchnutý v kontaktím poli, tak proto tento typ :-). Před operákem
jsou zařazeny potenciometry pro nastavení úrovně a strmosti hran. Signál z operáku je veden přes malý bezindukční odpor
na ADC0 vstup převodníku a zárověň do 10 MOhm sondy osciloskopu (kvůli nižší kapacitě). Sériový odpor byl nutný, protože OZ jinak kmital někde okolo 30 MHz.
Komunikace s PC je řešena klasicky přes UART bez parity s jedním stop bitem. Konkrétně jsem použil FT232 převodník a ten nějak neskousl
datový tok směrem do PC, takže jsem musel přidat řízení toku RTS. Btw se ukázalo, že FT232 tento signál používá ke zpomalení přenosu i když není aktivován v nastavení COM portu (Windoze XP)!
Firmware pro AVR je velmi jednoduchý. Jen nastaví ADC, timer PWM kanálu a UART. V přerušení od ADC je vzorkování+řazení vzorků do kruhového bufferu. Ten lze
přečíst příkazem 'W' přes UART. Odpověď MCU je word s počtem vzorků N a následuje N neznaménkových wordů průběhu s hodnotou 0 až 1023.
Program byl laděn v AVR Studiu 4.
AVR firmware a zdrojáky, 1.8.2013: ADC_bw_m644.zip (1.05 MB).
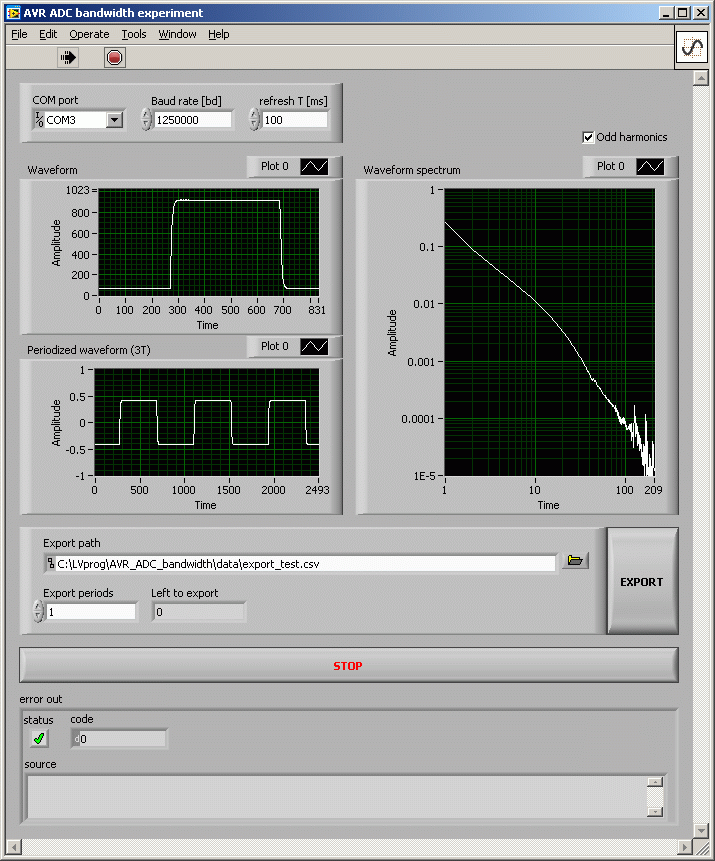 Fig. 2.2 - Rozhraní pro PC v LabVIEW 2011, signál f = 24.0674 kHz, fs = 12.019 kS/s, fs' = 20 MS/s.
|
LabVIEW rozhraní a "zdrojáky", V1.00, 31.7.2013: AVR_ADC_bandwidth.zip (1.05 MB).
Obr. 2.2 ukazuje screenshot jednoduchého GUI, které jsem pro účel zobrazení průběhu vytvořil.
Průběh na obrázku má kmitočet cca 24 kHz, reálný vzorkovací kmitočet je cca 12 kHz, ekvivalentní vzorkovací kmitočet 20 MHz.
Celkem 831 vzorků na periodu průběhu. Graf vpravo ukazuje amplitudy lichých harmonických průběhu.
Program je "napsán" v LabVIEW 2011, takže potřebuje ke spuštění runtime engine od NI a VISA ovladače. Oboje lze sosnout z webu
NI:
NI LabVIEW runtime engine 2012: http://joule.ni.com/nidu/cds/view/p/id/3433/lang/en,
NI LabVIEW VISA 5.3: http://joule.ni.com/nidu/cds/view/p/id/3823/lang/en.
Bohužel je toho docela dost, zvlášťe ty VISA drivery, ale prostě se mi nechtělo řešit grafy v C/C++ a LabVIEW je při této složitosti problému skutečně rychlé řešení. Bohužel nemám balík pro analýzu signálu a v základu není ani obyčejné FFT, takže jsem musel použít svoje vlastní DFT a byť jsem použil maticové operace (celé DFT je jen vynásobení dvou matic) tak to chodí nějak podezřele pomalu, ale pro 831 vzorků to ještě šlo. Program také umožňuje export zvoleného počtu period průběhu do souboru CSV.
Vlastní výpočet šířky pásma jsem pořešil skriptem pro GNU Octave. Mimojiné jsem použil funkci "leasqr()" z balíku "optim", takže to nepojede pod Matlabem, ale
prostě jsem nenašel nic, co by bylo v obou. Funkce se používá k proložení průběhu z DSO modelem, ze kterého vypadne kmitočtová odchylka časové základny DSO od AVR. Bez této korekce
by bylo měření nepoužitelné protože složky obou spekter, referenčního a z AVRka by na sebe "nesedly".
Hrubý postup výpočtu: Načtení průbehu z AVR a DSO ze souborů, preprocessing, korekce odchylky časové základny DSO od AVR, výpočet spekter z DSO a AVR, porovnání spekter => frekvenční přenos ADC.
Protože mě samozřejmě také zajímalo, jaký vliv na výsledný přenos mají nejistoty měření vstupních průběhů a parametrů, doplnil jsem analýzu nejistot měření Monte-Carlo metodou (MC). Analýza uvažuje jen
několik základních vstupů, jako je kvantizační šum, nelinearita ADC, zvlnění kmitočtového přenosu DSO a spol.
MC analýza nejistot je metoda hrubé výpočetní síly a potřebuje alespoň 1000 nebo lépe 10000 iterací, takže jsem použil vícejádrové výpočty.
Bohužel do dnes není pořešená implementace funkce "parcellfun()" pro Windoze, takže zbývá použít balík "multicore", který má ale jednu nevýhodu - distribuuje úlohy pomocí souborů ve sdílené složce.
Nevím jak na Linuxu, ale ve Windlích je to neskutečně pomalé i s malým množstvím předávaných dat, natož v tomto případě, kdy se předává celý průběh o délce řádově MB. Znamenalo by to 10000x duplikaci cca 8 MB souboru.
Z toho důvodu jsem vytvořil mezivrstvu, která seskupí iterace MC algoritmu do větších bloků, takže se parametry předávají třeba "jen" 100x. Tím se citelně snížila režie distribuce úloh pro jednotlivé výpočetní procesy,
takže se čtyřmi jádry je nárůst výkonu cca 3.1x proti jednomu a to včetně nechutně dlouhého startu procesů GNU Octave (poslední verze nabíha cca 30 s ... jo, kde jsou ty časy, kdy to naběhlo za 2 s i na úplném střepu ...).
Skrip jsem napsal v GNU Octave 3.6.4 s balíky "optim 1.2.2" a "multicore 0.2.15" (oba v základní instalačce pro Windoze).
GNU Octave scripty pro výpočet šířky pásma AVR ADC: Octave_AVR_ADC_bandwidth.zip (315 kB).
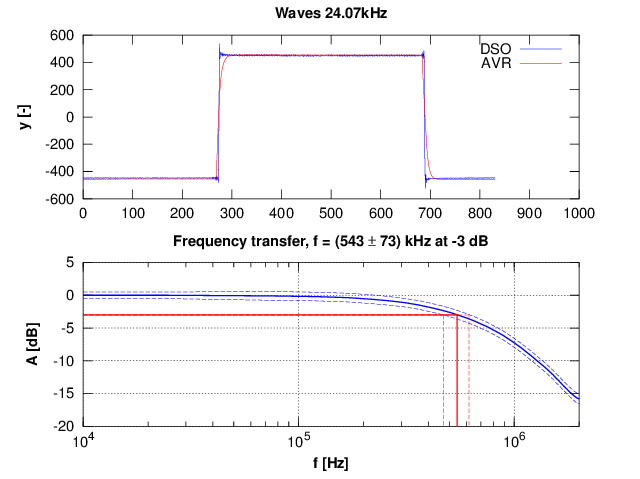 Fig. 2.3 - Změřená šířka pásma AVR ADC, signál f = 24.0674 kHz, fs = 12.019 kS/s, fs' = 20 MS/s, 831 vzorků na periodu.
|
Obr. 2.3 ukazuje výsledek výpočtu. Referenční signál je zde vzorkován low-end DSO od rákosky Owon DS7102V s kompenzovanou sondou Testec MF312 (250 MHz). Vzorkovací kmitočet DSO je 500 MS/s real-time. DSO je sice hodně low-end, ale má šířku pásma cca 100 MHz, takže v oblasti zájmu okolo 1 MHz by měl mít charakteristiku celkem slušnou. Změřená šířka pásma pro pokles o 3 dB je (543 ± 73) kHz. Rozložení pravděpodobnosti nejistoty měření je na obr. 2.4.
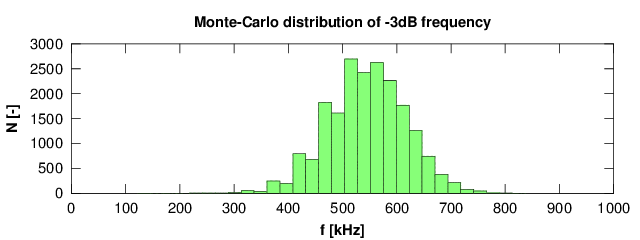 Fig. 2.4 - Změřená šířka pásma AVR ADC, rozdělení pravděpodobnosti nejisoty měření.
|
Pokus jsem zopakoval pro různé kmitočty průběhu, nižší i vyšší, i s pomalejšími hodinami ADC, ale vždy to vyšlo prakticky stejně (v rámci nejistot), takže pokud jsem se nějak zásadně nespletl v algoritmu, tak to asi bude reálný výsledek. Celkem by to i odpovídalo vzhledu průběhu proti DSO. ADC převodník AVR je tedy pro účely měření true-RMS hodnoty proudu s kmitočtem okolo 40 kHz více než dostatečný (signál neobsahuje nijak významné vyšší kmitočtové složky).
| Last update: 5.8.2013 |  |
 |