Rychlá Fourierova transformace (FFT) pro AVR

   FFT je sice obvykle počítána na rychlých DSP, které jsou k tomu instrukční sadou podstatně lépe přizpůsobeny, nicméně MCU řady AVR, přestože jen 8-bitové, poskytují dostatek výkonu pro celkem svižný výpočet v pevné řádové čárce. Pokud se algoritmus má vejít do interní RAM, tak je jeho rozlišení značně omezeno, resp. je třeba volit kompromis mezi přesností výpočtu a rozlišením transformace. Asi úplné minimum, kdy má smysl se o FFT pokoušet, je 16-bit rozlišení, kde pro 4kB interní RAM může být maximální rozlišení FFT 512 bodů (je třeba počítat s pamětí pro stack MCU). Poměrně zdařilá implementace FFT pro AVR se, jako řada dalších zajímavých věcí, nachází na známém webu www.elm-chan.org. Jedná se o algoritmus DIF radix 2 (decimace ve frekvenci se základem 2). Uvedený kód ale není nijak zvlášť optimalizovaný a než bych ho zkoumal a upravoval, tak jsem se rozhodl to napsat rovnou znovu a jinak. Pro svou implementaci jsem zvolil metodu DIT (decimace v čase), která se mi zdá o fous méně náročná na čas MCU.

  1. Něco teorie k Fourierově transformaci
  2. Realizace FFT na AVR (AvrAsm32 assembler)
  3. Realizace FFT na AVR (AVR GCC)


1. Něco teorie k Fourierově transformaci

1.1 FFT vs. DFT

   Než se pokusím popsat samotný algoritmus FFT, asi by nebylo od věci vysvětlit, co to vlastně je diskrétní Fourierova transformace (DFT). Teorie na toto téma je plný internet (občas i česky), takže jen stručně. Jde o transformaci signálu z časové oblasti do frekvenční oblasti, tj. vstupem do DFT je diskrétní navzorkovaný signál a výstupem diskrétní spektrum tohoto signálu - informace o frekvenčních složkách v něm obsažených. Jak vstup, tak i výstup (obraz) transformace je v komplexním tvaru. Matematicky je DFT definována takto:



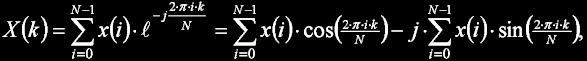
kde N je velikost transformace. Celkem je třeba provést N2 komplexních součinů, což je dost zdlouhavé. Naštěstí má ale DFT jednu pěknou vlastnost - pro reálný vstupní sígnál o sudém počtu prvků je spektrum symetrické a komplexně sdružené kolem svého středu, takže reálná složka je kolem středu sudá a imaginární složka lichá. Stačí tak vypočíst první polovinu spektra a druhá bude identická s opačným znaménkem u imaginární složky:



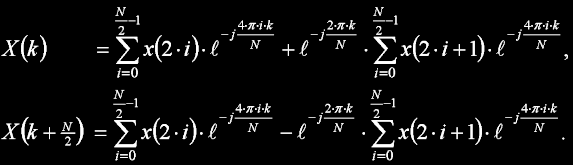
   Původní DFT o délce N se rozdělila na dvě DFT o polovičních délkách, kde jedna je počítána ze sudých a druhá z lichých členů vstupní posloupnosti. Tím se celkový počet komplexních součinů snížil na polovinu a zároveň se o nic nepřišlo. Pokud má vstupní posloupnost délku N=2M, lze DFT takto půlit dál až zbyde N/2 jednoduchých DFT velikosti 2 (řád 1), které se podle digramu říká motýlek (v tomto případě Decimation In Time - DIT):

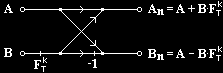kde A a B jsou vstupní a výstupní hodnoty DFT a FTk je zkráceně zapsaná exponenciála z předchozího vztahu (bývá označována jako "twiddle faktor"):



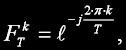
kde k/T představuje úhel twiddle faktoru. Násobení vstupu B tímto členem není nic jiného, než jeho rotace v komplexních souřadnicích (vektorová rotace vyjádřená v polárním tvaru). Poněkud průhledněji tato operace vypadá ve složkovém tvaru:



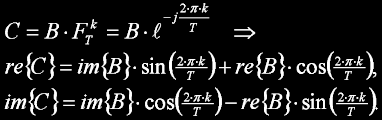
   Kompletní DIT motýlek ve složkovém tvaru pak vypadá takto:



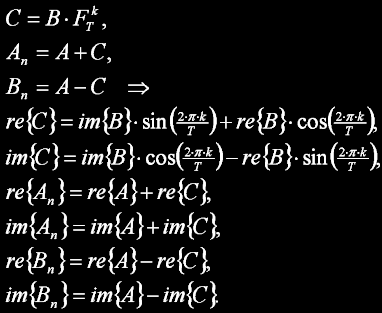
   Jak je vidět, tak výpočet neobsahuje žádnou aritmetickou záludnost, jen čtyři násobení a 6 součtů - nic, co by 8-bit MCU nezvládl. Hodnoty sin() a cos() jsou navíc často předpočtené v tabulkách, takže skutečně bez problému.

1.2 Inverzní DFT

   Jak se asi dá očekávat, tak DFT má, stejně jako spojitá verze, i inverzní variantu, která ze spektra (obrazu) zpětně rekonstruuje vstupní sígnál (předlohu). Změna proti dopředné transformaci spočívá pouze ve změně směru rotace twiddle faktoru z FTk na FT-k. DIT motýlek pak bude vypadat takto:



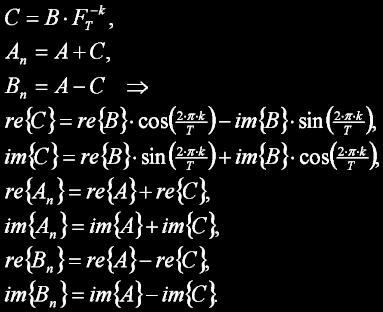
   Pokud má mít rekonstruovaný signál identickou amplitudu, jako měl před provedením výše uvedeného DFT, pak je navíc třeba provést normalizaci násobením získaného signálu koeficientem 1/N.


1.3 FFT Cooley - Tukey DIT radix 2

   Takto je označován zřejmě nejrozšířenější algoritmus pro výpočet rychlé Fourierovy transformace (FFT). Je poskládán kompletně z výše popsaných motýlků. Algoritmus je použitelný pouze pro délku vstupní posloupnosti N=2M (základ 2 neboli "radix 2"). Celý výpočet je dělen na etapy, kterých je M=log2(N) a v každé etapě je vypočteno N/2 motýlků, takže M*N/2 motýlků celkem, tj. 2*M*N násobení a 3*M*N součtů. Příklad tohoto algoritmu pro N=8 (M=3 etap):


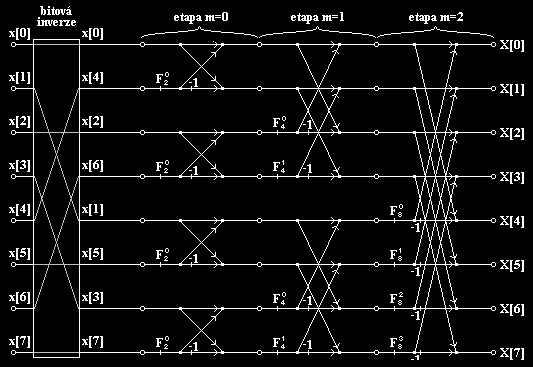   Pokud má být algoritmus programově efektivně realizovatelný, tak je nejprve třeba vhodně přeskládat prvky vstupní posloupnosti. Této úpravě se říká bitová inverze - obrátí se pořadí bitů v adrese vstupního prvku:

Bitová inverze pro M=3
Původní pozice Nová pozice
dec bin bin dec
0 000 000 0
1 001 100 4
2 010 010 2
3 011 110 6
4 100 001 1
5 101 101 5
6 110 011 3
7 111 111 7

   Je to sice poněkud nepříjemná operace (zejména má-li se provádět v rámci jednoho pole), nicméně algoritmus FFT pak může proběhnout na místě, tj. v rámci jednoho pracovního pole, což je na MCU s malou RAM nutnost. Výstup výše uvedeného algoritmu je již naštěstí ve správném pořadí.
   Drobnou nepříjemností algoritmu je, že se v jeho jednotlivých etapách struktura mění (mění se poloha a vzdálenost vstupů motýlku), nicméně dá se to poměrně obstojně zvládnout pomocí dvou pointerů. Vlastní FFT tohoto typu na již správně přeskládaných datech by v C mohla vypadat přibližně takto: 

#define N 8

typedef struct{
    double re;
    double im;
}TCplx;

double tsincos[N]={0.000, 1.000, 0.7071, 0.7071, 1.000, 0.000, 0.7071,-0.7071};
TCplx FFTwarr[N];

void FFTditR2(void)
{
    double dsin,dcos;
    double *Fnk;
    TCplx C;
    TCplx *A,*B;
    int s,k;
    int n=1;
    int angf=N/2;
        
    while(n<N)
    {
        A=&FFTwarr[0];
        B=&FFTwarr[n];     
        Fnk=&tsincos;
        
        for(k=0;k<n;k++)
        {
            dsin=*Fnk++;
            dcos=*Fnk++;
            
            for(s=0;s<angf;s++)
            {
                C.re=B->im*dsin + B->re*dcos;
                C.im=B->im*dcos - B->re*dsin;
                B->re=A->re - C.re;
                B->im=A->im - C.im;
                A->re=A->re + C.re;
                A->im=A->im + C.im;
                A+=2*n;
                B+=2*n;              
            }
            A-=(N-1);
            B-=(N-1);             
            Fnk+=(angf-1)*2;
        }        
        n<<=1;
        angf>>=1;
    }
}

   Hodnoty twiddle faktoru pro jednotlivé úhly jsou již předpočteny v poli tsincos[]. Vnitřní smyčka provádí vlastní výpočet motýlku pro každou sekci s etapy. Nadřazená smyčka toto zopakuje pro každý úhel twiddle faktoru resp. pro každé posunutí k motýlku vůči začátku sekce s. Nejvyšší smyčka toto celé opakuje pro každou etapu výpočtu m - v každé další etapě je vzdálenost mezi vstupy motýlku n dvojnásobná a frekvence rotace úhlu twiddle faktoru angf poloviční. Graficky znázorněný význam jednotlivých proměných pro druhou etapu výpočtu:



1.3.1 Možnosti optimalizace

   Pokud by bylo třeba jít do extrému, tak lze ušetřit trochu strojového času vypuštěním násobení z výpočtu motýlku v případě, že úhel twiddle faktoru je 0 nebo pi/2, kdy hodnoty sin() a cos() nabývají pouze hodnot 0, -1 a +1. Pro úhel 0 by motýlek vypadal takto:



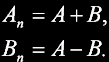
   Pro úhel pi/2 by motýlek vypadal takto:



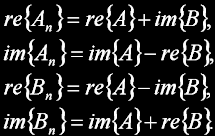
   První vztah lze použít pro celou první etapu výpočtu a dále vždy pro k=0. Druhý vztah lze použít od druhé etapy pro k=(n>>1). Na PC tato úprava nic moc nepřinese, ale na 8-bit MCU rozhodně ano (na AVR v přesnosti 16-bit trvá komplexní násobení twiddle faktorem cca 80cyklů).


1.4 Fourierova transformace a okna

   Protože vstupem ke spektrální analýze je prakticky vždy neperiodický signál, tj. obecná řada vzorků o libovolné délce, je třeba před vlastní DFT provést jeho periodizaci - výběr úseku ke zpracování. To se provádí pomocí okénkových funkcí. Nejjednodušší funkcí je obdélníkové okno, které realizuje prostý výřez úseku ze zdrojové posloupnosti bez úpravy jeho amplitudy. Při výběru úseku mohou nastat dvě situace. Buďto na sebe začátek a konec vybraného úseku spojitě a hladce navazuje nebo ne. V prvním případě nebude s analýzou pomocí DFT problém, protože periodizovaný signál nebude obsahovat žádné strmé přechody. Tento případ ale v reálu nastane málokdy (s ohledem na zcela náhodný charakter analyzovaného signálu) a periodizovaný signál tak bude často obsahovat nespojitosti:


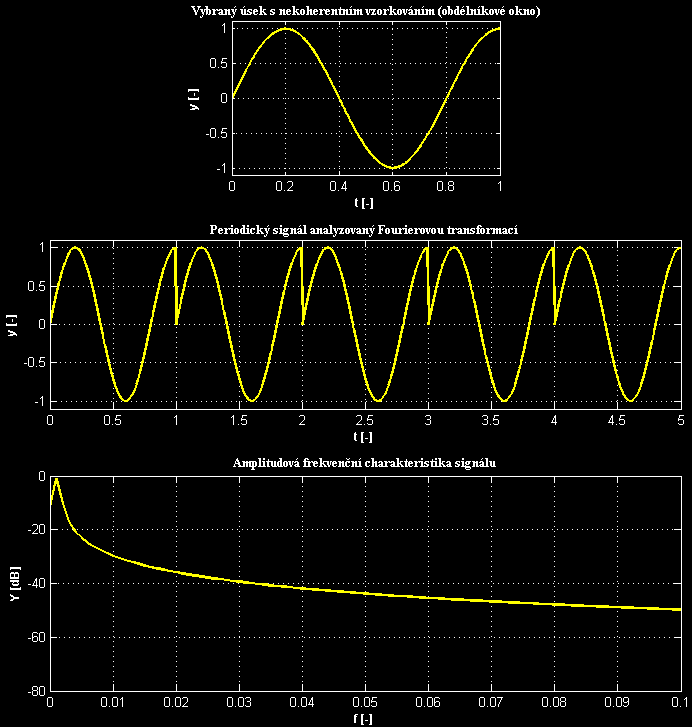   První graf ukazuje výběr (obdélníkové okno) úseku ze sinusového průběhu, vzhledem k délce úseku má signál frekvenci 1,25 (tedy nekoherentní vzorkování). Druhý průběh ukazuje pár period periodizovaného signálu (získáno opakováním vybraného úseku) - to je průběh, který ve skutečnosti "vidí" DFT. Výsledné spektrum pak obsahuje jasně patrný peak signálu o frekvenci 1,25, ale také všechny frekvenční složky odpovídající nespojitosti v analyzovaném signálu. Frekvenční složky s menšími amplitudami by se zcela ztratily.
   Řešením tohoto problému je použití okna, které kromě výběru navíc vhodně upravuje amplitudu signálu (násobení signálu oknem). Jednou z možností je např. velmi jednoduché Hannovo okno, jehož průběh je v grafech naznačen tečkovaně:


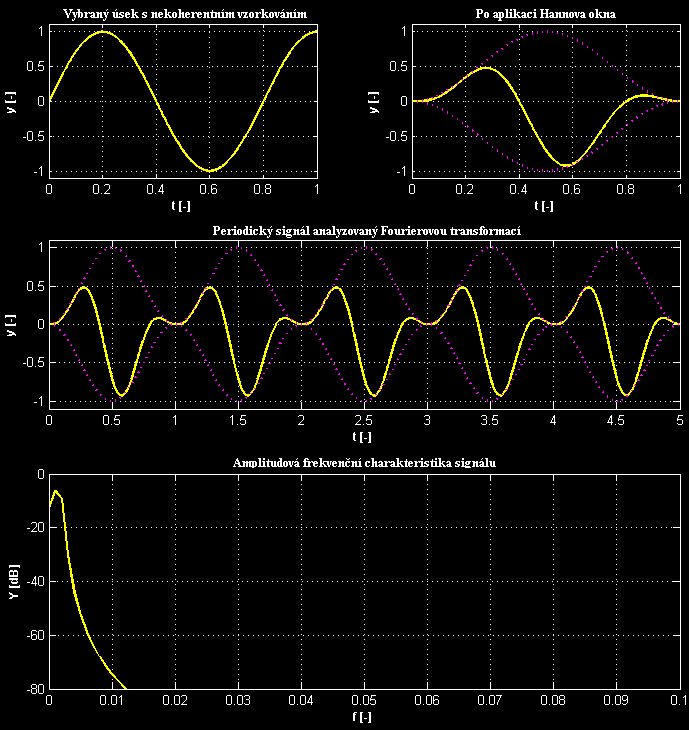   Záčátek i konec úseku na sebe hladce navazuje, periodizovaný signál neobsahuje žádné nespojitosti a spektrum je tak podstatně čistší. Bohužel Hannovo okno, stejně jako každé jiné, má svoje vlastní spektrum a to se pochopitelně přičte ke spektru analyzovaného signálu (násobení předloh je ekvivalentní konvoluci spekter). Výsledkem je rozložení/prosáknutí energie analyzovaného signálu do širšího frekvenčního pásma a s tím související změna amplitudy hlavního peaku protože celková energie musí zůstat zachována. Díky tomu se např. mohou "slít" dva blízké peaky do jednoho.
   Některá běžně používaná okna a jejich vlastnosti jsou uvedeny v následující tabulce:

Parametry vybraných okénkových funkcí
Název Průběh CG CW SLA SLD
- - - bin dB dB/okt
Hann 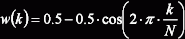0,5 ±1 -32 -60
Hamming 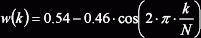0,54 ±1 -43 -20
Blackman 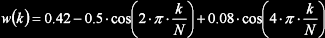0,42 ±2 -58 -60
Blackman-Harris 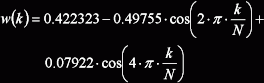0,422 ±2 -67 -20
Blackman-Nuttall 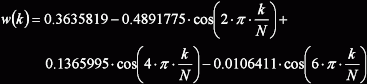0,364 ±3 -98 -20

CG ... koeficient zesílení hlavního peaku při koherentním vzorkování
CW ... počet postranních peaků při koherentním vzorkování
SLA ... amplituda nejbližšího postranního laloku
SLD ... strmost poklesu amplitudy potranních laloků

   Obecně platí, že čím bohatší je spektrum okna, tím menší amplitudu má jeho nejbližší postranní lalok. Průběhy uvedených oken:

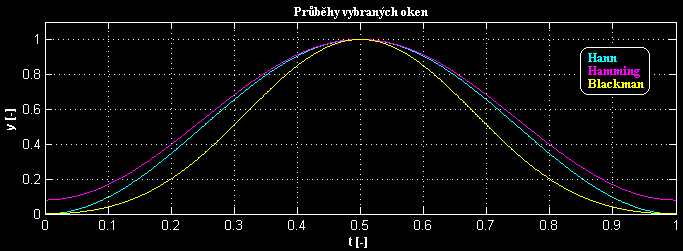
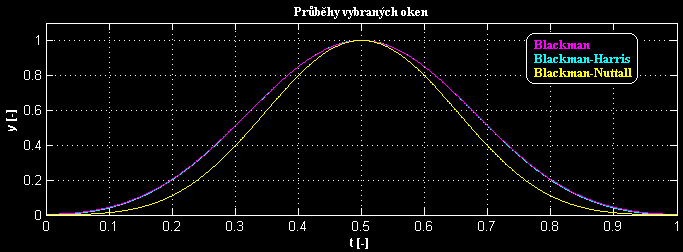
   A jejich spektra (1 bin = 0,01):


2. Realizace FFT na AVR (AvrAsm32 assembler)

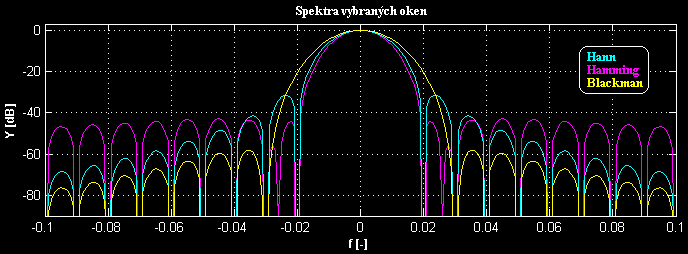
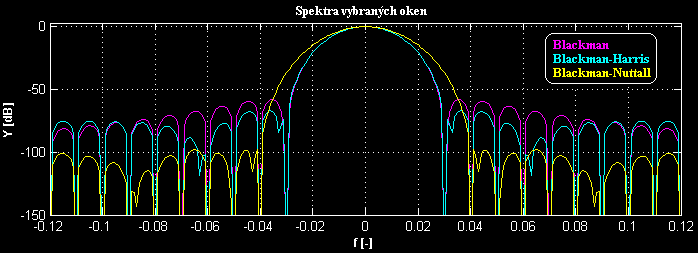
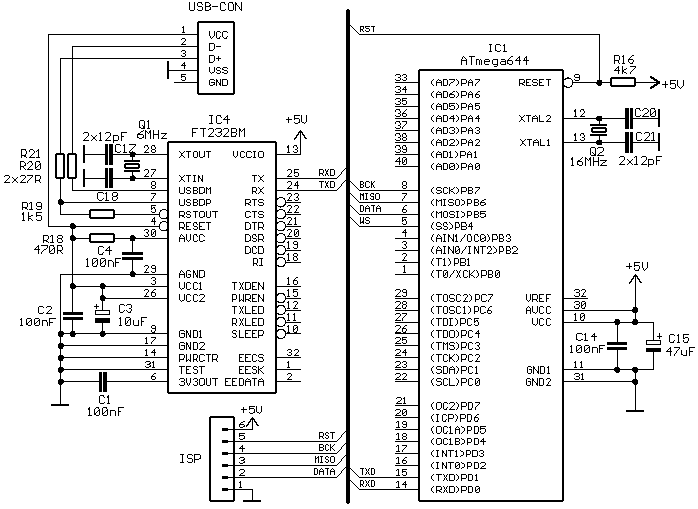
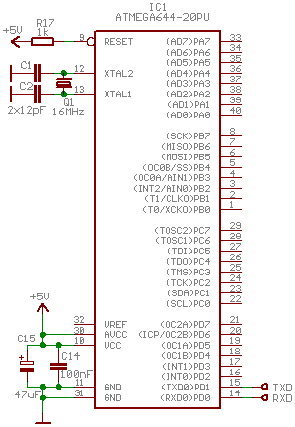
   Nyní už k vlastní realizaci na AVR. Kvůli potřebné RAM jsem zvolil ATmega644, která jí má 4kB (nejvíce v DILku). Protože pokoušet se o ladění FFT s vykreslováním na LCD je poněkud nepraktické, rozhodl jsem se napsat prográmek pro Windows XP, který slouží jako grafické rozhraní. S ním zařízení komunikuje jako obvykle po sériovém portu resp., kvůli rozumné odezvě, přes virtuální USB-COM port. Přenosová rychlost je nastavená na maximální 2MBd @ XTAL=16MHz bez parity. Původně jsem předpokládal, že bude třeba použít řízení toku směrem do PC, protože FT232BM má pouze 384/128B FIFO, ale systém si s tím nějak očividně poradil i při 1024B blocích dat. Doplnit testování RTS linky v rutině "UsTxByte" by ale v případě potřeby neměl být problém.


   Program pro PC je napsán v prostředí BDS 2006 - Turbo C++ a testován pouze v XP. Co to bude dělat v novějších OS netuším, ale práce s COM portem snad zůstala zpětně kompatibilní. Před použitím programu je třeba nastavit číslo COM portu a baudrate v souboru "config.ini". Program je vybaven timeouty, takže v případě problémů s komunikací by neměl vytuhnout. Případné problémy se sekáním komunikace by mělo řešit nastavení latence USB-COM převodníku přímo v ovladačích.

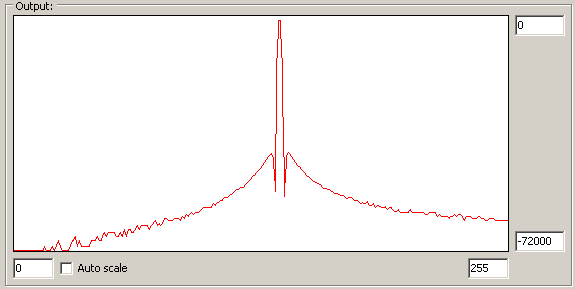
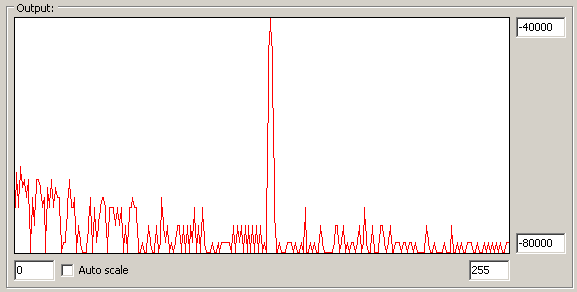
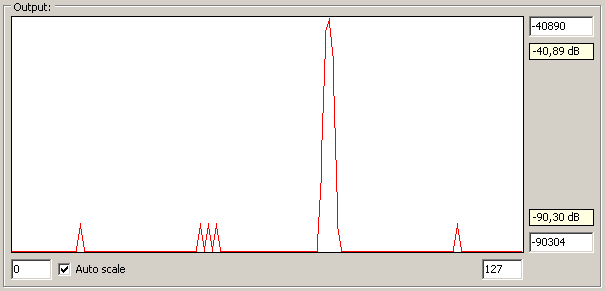
   Prográmek předně obsahuje jednoduchý signálový generátor, parametry lze měnit scrollbarem nebo ručně zadat. Vygenerovaný signál je zobrazen v horním grafu. Dále lze nastavit, co má MCU spočítat. Jednak je zde možnost zobrazit časový průběh po aplikaci okna ("time domain"), dále lineární amplitudové spektrum ("frequency domain"), případně logaritmické amplitudové spektrum a nakonec zase logaritmické, ale s logaritmem vypočteným na PC (pro přesnější výsledky). Výsledek je zobrazen ve spodním grafu. U logaritmického měřítka je y-osa udaná v dB*1000. U obou grafů lze ručně zadat rozsah y-osy (hodnotu potvrdit stiskem "Enter"). Stisk "Enter" v prázdném poli nastaví zpět defaultní hodnotu.
   Poslední věcí, co prográmek umí, je výpis nastavení FFT na MCU a výpis statistik, tj. především změřené časy. Výpis změřených časů pro různá nastavení FFT ukazuje následující tabulka:

Rychlost mé implementace FFT pro XTAL=16MHz
FFTN FFTopt Výstup FFTinit FFTditR2 FFTout Celkem Výkon
- - - ms ms ms ms kp/s
32 0 lin 0,118 0,707 0,601 1,426 22,440
log 0,118 0,707 0,655 1,480 21,622
1 lin 0,118 0,500 0,601 1,218 26,273
log 0,118 0,500 0,655 1,272 25,157
64 0 lin 0,235 1,670 1,203 3,108 20,592
log 0,235 1,670 1,305 3,210 19,935
1 lin 0,235 1,251 1,204 2,690 23,796
log 0,235 1,250 1,306 2,791 22,931
128 0 lin 0,485 3,855 2,410 6,750 18,963
log 0,485 3,855 2,613 6,953 18,408
1 lin 0,485 3,012 2,409 5,906 21,673
log 0,485 3,012 2,609 6,106 20,963
256 0 lin 0,969 8,745 4,821 14,535 17,613
log 0,969 8,745 5,227 14,941 17,143
1 lin 0,969 7,057 4,820 12,845 19,930
log 0,969 7,056 5,216 13,241 19,334
512 0 lin 1,937 19,567 9,643 31,147 16,438
log 1,937 19,567 10,485 31,962 16,019
1 lin 1,937 16,190 9,643 27,769 18,437
log 1,937 16,190 10,431 28,558 17,928

   Časy jsou měřeny pro FFTprec=0 a přesnou rutinu odmocniny (viz. popis SW pro MCU), tedy stejnou, jako používá implementace AVRFFT (z webu www.elm-chan.org). FFTopt zapíná optimalizaci pomocí zjednodušených motýlků (opět viz. popis níže). Nárůst výkonu pro FFTopt=1 při FFTN=256 je cca 24%, což je celkem slušný efekt. Pro menší FFTN je nárůst výkonu ještě výraznější. Konkrétně pro FFTN=256 a lineární výstup je moje implementace asi o 7,3% (resp. o 21% pro FFTopt=1) rychlejší oproti AVRFFT. Při zvýšené přesnosti výpočtu (FFTprec=1) bude výkon asi o 12% nížší (a odstup signál/šum asi o 8dB vyšší). Význam prvků tabulky by měl být zřejmý z níže uvedného popisu SW pro MCU.

Program ke stažení: AVR_FFT_tester.zip (320kB).


2.1 SW pro MCU

   Firmware pro MCU je napsán kompletně v ASM, nicméně ty podstatné funkce realizující FFT nemají parametry, takže přepracování do "*.s" funkcí pro jazyk C není problém (jen bude asi problém s některými direktivami použitého překladače AVRasm32). Kód je pro přehlednost rozdělen do několika modulů, které budou popsány dále.

Zdrojáky ke stažení: SM_AVR_FFT.zip (42kB).


2.1.1 Modul "FFTditR2.asm"

   Zde jsou umístěny rutiny vlastní FFT transformace. Všechny pracují s jediným pracovním polem FFTwarr[] word prvků, zapsáno v C:

int16 FFTwarr[FFTN*2];

přičemž FFTN je velikost FFT. Toto pole je komplexní (proto *2), přičemž sudé prvky představují realné hodnoty (v textu označované jako re{FFTwarr[]}) a liché imaginární (v textu jako im{FFTwarr[]}).
   Použití toho modulu je zhruba následující:

  1. Naplnit pole re{FFTwarr[]} reálnou zdrojovou řadou dat o délce FFTN. Data musí být v 16-bit znaménkovém tvaru. Druhou část pole im{FFTwarr[]} nechat jak je, bude přepsána.

  2. Zavolat rutinu "FFTinit", která provede bitovou inverzi adres a aplikuje na data okno (pokud tedy není vybráno obdélníkové), výsledek uloží do im{FFTwarr[]} a následně zduplikuje zpět do re{FFTwarr[]} - je to asi nejlepší způsob, jak to provést relativně rychle a neplýtvat přitom RAM na pomocný buffer.

  3. Zavolat rutinu "FFTditR2", která provede vlastní FFT transformaci. Vše probíhá na místě, takže po skončení této rutiny obsahuje pole FFTwarr[] komplexní spektrum (už ve správném pořadí).

  4. V případě potřeby zavolat rutinu "FFToutLin", která z komplexního spektra vytvoří lineární amplitudové spektrum. Výsledné spektrum je uloženo zpět do pole FFTwarr[], ale tentokrát už ne na sudé adresy (do re{}), ale pořadě, tj. od prvku 0, do FFTN/2-1 (je vypočtena pouze polovina spektra - druhá polovina je identická). Pro fullscale vstupní signál a obdélníkové okno se amplitudy spektra pohybují od 0 do 32768, při použití jiných oken jsou adekvátně nižší, viz. výše.

  5. Eventuleně MÍSTO "FFToutLin" zavolat "FFToutLog", která provede sice totéž, ale v logaritmickém měřítku. Tato rutina vrací znaménkové výsleky přímo v dB ve fixed point formátu (fx 8.8). Logaritmování je zde realizováno rutinou "log10f" z modulu "math.asm". Tato rutinka provádí s lineární amplitudou x=r zhruba toto:



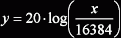
    kde číslo 16384 představuje hodnotu x odpovídající výstupu y=0dB. Všechno nad toto číslo je ořezáno na 0dB a nejnižší hodnota y je ořezána na cca -88dB. Zmíněná rutinka je těžce experimentální, takže výsledky mohou mít poměrně nepříjemné odchylky, ale zato je slušně rychlá.

   Všechny rutiny by měly být funkční pro FFTN={32, 64, 128, 256, 512}. V případě doplnění lookup tabulek i pro menší rozsah, ale rozhodně ne pro vyšší. Už pro FFTN=512 je v kódu spousta preprocesorového balastu, protože už prostě nezbylo dost registrů na rozšíření všech potřebných proměnných na 16-bit a práce s proměnnými v RAM je poněkud pomalá.
   Šum se pohybuje okolo -70dB vůči maximu r=32768. Duplikace zdrojového signálu do obou komplexních složek odstup sice o nějaké ty 3dB vylepšuje, ale i tak to není nijak úchvaný výsledek. Konkrétně je to způsobeno použitím aritmetických rotací. Aritmetická rotace vpravo totiž není identická s dělením dvěma - chce to doplnit korekci výsledku pro negativní čísla (př.: -3/2=-1, ale -3>>1=-2). To si ovšem vyžádá nezanedbatelné množství výkonu MCU. Z toho důvodu jsem doplnil přepínač FFTprec, který v případě potřeby maximální přesnosti umožňuje tyto korekce zapnout (umístěn v modulu "main.asm"). Šum se sníží na nějakých -78dB, ale bude to asi o 12% pomalejší.
   V modulu jsou ještě rutiny "FFTrxData"/"FFTtxData", které slouží ke komunikaci s PC (příjem dat ke zpracování a odeslání zpracovaných dat).


2.1.2 Modul "FFTditR2tables.asm"

   Zde jsou všechny lookup tabulky potřebné pro FFT pro různé velikosti FFTN. Předně je zde tabulka TFFTbrv, která obsahuje předpočítané koeficienty pro bitovou inverzi (pro FFTN≤64 8-bit, jinak 16-bit).
   Dále tabulka TFFTsico, která obsahuje znaménkové hodnoty sin(w) a cos(w) pro w=0...pi v FFTN/2 krocích (hodnoty jsou řazeny střídavě: sin, cos, sin, cos, ...). Amplituda je fullscale 16-bit, tj. ±32767.
   Nakonec jsou zde tabulky okénkových funkcí TFFTwdw. Ty obsahují průběh okna ve FFTN krocích ve znaménkovém 16-bit formátu, tj. ±32767.
   Z optimalizačních důvodů mohou být hodnoty sin() jen kladné (to asi není problém :-) a hodnoty oken defaultně rovněž jen kladné (co by člověk neudělal pro pár ušetřených cyklů při násobení :-). Pokud by bylo třeba použít okno s oběma polaritami hodnot (třeba flattop), tak je nutné v modulu FFTditR2.asm nastavit "FFTwsign=1" (bude to o fous pomalejší).
   Protože generovat všechny tyto tabulky ručně by asi byl problém, napsal jsem jednoduchou utilitku, která vysype všechny potřebné tabulky pro AVR assembler (někdy i ve více variantách). Napsáno a testováno je to jen v XP, ale snad to bude chodit i na novějších OS.
   Použití je velice prosté: "AVRFFTlookup.exe FFTN" vygeneruje lookup tabulky pro FFT velikosti FFTN.

Utilitka ke stažení: AVRFFTlookup.zip (64kB).


2.1.3 Modul "FFTmacros.asm"

   Nějaká ta makra různých násobení a také makra obsahující zjednodušený motýlkový algoritmus pro úhly 0 a pi.


2.1.4 Modul "math.asm"

   Zde jsou rutiny složitější aritmetiky. Předně 32-bit odmocnina stažená z www.elm-chan.org ("tech. notes" sekce). Tahle rutinka je přesná, zato ale dost pomalá (cca 550 cyklů). Z toho důvodu jsem se rozhodl zkusit to rychleji přes lookup tabulky s omezenou přesností a celkem se to i povedlo. Funguje to zhruba tak, že se vstupní proměnná x rozdělí na část indexovací (výběr prvku z lookup) a část zlomkovou, která slouží k linární interpolaci mezi prvky lookup. Pro 8-bit vstup je přesnost absolutní (vrací to zaokrouhlenou hodnotu) pro 16-bit a více je chyba pod 0,6%. Kvůli vyšší přesnosti je lookup rozdělena na dvě části s různým rozlišením.
   Dále je zde již zníměná rutina dekadického logaritmu. Možnosti jak rychle vypočíst logaritmus jsou v zásadě jen dvě. Předně iterační, kdy se prohledává lookup na hodnotu nejbližší vstupu x a podle toho, kde se tato hodnota v lookup nachází se přiřadí výstup y. Tuhle metodu používá např. právě FFT spektrální analyzátor z webu www.elm-chan.org. Bohužel rozlišení výstupu je dost omezené. Na vykreslení spektra na malé LCD jistě dostačující, ale pro přesnější výstup by bylo třeba použít interpolaci ze sousedních hodnot lookup a ta se, v tomto případě, neobejde bez 32-bit dělení, což je na AVR extrémně zdlouhavá záležitost.
   Druhá možnost je přímá metoda, tj. stejný princip, jako výše uvedená odmocnina a tuto metodu jsem použil pro napsání rutiny "log10f". Ta se vstupní proměnnou x provede následující výpočet:



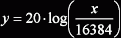
kde 16384 představuje hodnotu vstupu x pro kterou je vráceno y=0dB. Vše nad 0dB je oříznuto a vše pod cca -88dB rovněž. Výstup je ve fixed point formátu (fx 8.8) přímo v dB. Protože logaritmus je svým průběhem ještě horší funkce než odmocnina, tak jsem musel lookup tabulky rozdělit do tří částí s různými rozlišeními. Díky tomu je ale přesponst poměrně slušná - chyba pod 0,2% s výjimoku nejnižších amplitud, kde je funkce dost nelineární (a tudíž lineární interpolace nemá šanci).
   Rutinka je opatřena lookup tabulkami pro použití Hannova okna, tj. pro amplitudovou korekci CG=0,5, takže proto je maximum nastaveno na 32768*CG=16384. Při použití jiných oken je třeba vygenerovat jiné tabulky, ideálně pomocí níže uvedené utilitky. Testováno opět jen v XP, takže na novějších OS bez záruky. Použití je následující:
"log10lookup.exe db0 dbmax",
kde db0 je hodnota x pro y=0dB a dbmax maximální hodnota x. Uvedená rutinka může vracet i kladná čísla, tj. např. pro db0=16384 a dbmax=32768 bude rozsah y = -90dB až +6dB.

Utilitka ke stažení: log10lookup.zip (64kB).
Test přesnosti rutiny v porovnání s výpočtem na PC: log10f_test.zip (90kB).


2.1.5 Modul "main.asm"

   Zde jsou jen rutiny pro použití USARTu a vlastní komunikační protokol s PC. Ten vypadá z pohledu MCU zhruba takto:

  1. Čekat na příkaz (pro začátek FFT je kód znak 'F').
  2. Odeslat kladnou odpověď 'A', případně zápornou 'E' v případě neznámého příkazu.
  3. Příjmout byte parametru příkazu, kde:
    bit0 - určuje, jestli bude vypočteno spektrum (frekvenční oblast - 1) nebo jen aplikováno okno a bitová inverze (časová oblast - 0)
    bit1 - určuje, jestli bude výstup v lineárním (0) nebo logaritmickém (1) měřítku.
  4. Odeslat word udávající velikost FFT FFTN.
  5. Odeslat dword udávající frekvenci krystalu XTAL.
  6. Odeslat byte udávající vybrané okno:
    0 - Hann, 1 - Hamming, 2 - Blackman, jinak obdelník.
  7. Příjmout signál ke zpracování, tj. FFTN znaménkových wordů.
  8. Odeslat synchronizační znak 'D'.
  9. Odeslat word obsahující dobu výpočtu "FFTinit" v cyklech timeru (XTAL/8).
  10. Odeslat word obsahující dobu výpočtu "FFTditR2" v cyklech timeru (XTAL/8).
  11. Odeslat word obsahující dobu výpočtu "FFTout???" v cyklech timeru (XTAL/8).
  12. Odeslat výsledeky, tj. pro časovou oblast FFTN znaménkových wordů a pro frekvenční oblast FFTN/2 neznaménkových wordů (první polovina amplitudového spektra).

   Kromě uvedeného jsou zde všechny podstatné přepínače preprocesoru. Jednak klasicky frekvence hodin XTAL v Hz, dále FFTN jakožto zvolená velikost FFT, FFTwindow udávající typ okna, FFTopt, který umožňuje zakázat použití zjednodušených motýlků (ušetří se nějaká ta FLASH, ale bude to pomalejší), FFTprec, který zapne korekci po aritmetické rotaci pro vyšší odstup signál/šum a nakonec FFTfsqrt, kterým se vybírá mezi přesnou/rychlou rutinou odmocniny.




3. Realizace FFT na AVR (AVR GCC)

   Poměrně nedávno jsem se přinutil začít experimentovat s AVR GCC a protože jsem si chtěl trochu procvičit kombinování assembleru se zbytkem projektu v C, rozhodl jsem se přepracovat původní assemblerovskou implementaci FFT pro AVR GCC. Pokud mohu soudit, tak se to celkem i zdařilo a nepodepsalo se to nijak znatelně ani na velikosti zdrojáku. Při té příležitosti jsem rovněz opravil pár chybek a nedostatků, především vlastní DIT motýlek který, jak jsem byl upozorněn, generuje opačné znaménko u imaginární složky. Vzhledem k tomu, že jsem počítal amplitudové spektrum, tak se to pochopitelně neprojevilo, ale pro korektnost jsem raději algoritmus opravil.
   Projekt je svojí funkcí prakticky identický s původní implementací, jen jsou jeho kostra a časově nenáročné operace v C, takže je poněkud čitelnější. Do vlastní implementace v assembleru prakticky není třeba zasahovat, jedině snad v případě, že by bylo třeba přidat další okna nebo jiná rozlišení.


3.1 Testovací program pro PC

   Komunikace by měla být kompatibilní i s původní verzí programu, ale raději bych použil novou, lehce vylepšenou verzi (ke stažení dále). Bylo opraveno pár chybek, přidáno menu s možností testování algoritmů sqrt32f() a log10f() a rovněž něco informací o signálu a spektru navíc. Nastavení zůstalo stejné, tj. stací zadat číslo COM portu a baudrate.

Ukázka výstupu pro FFTN=256, sinus -40dB, FFTprec=1.
Ukázka výstupu pro FFTN=256, sinus -40dB, FFTprec=0.

Program ke stažení: AVR_FFT_tester_v2.zip (365kB).


3.2 AVRFFT pro AVR GCC

   K vlastní implementaci AVR FFT patří pouze následující soubory:

  1. "FFT_routines.s" - vlastní rutinky FFT transformace
  2. "FFT_macros.inc" - vyšší makra pro FFT algoritmus
  3. "FFT_tables.inc" - lookup tabulky FFT algoritmu
  4. "FFT_math.s" - rychlá aritmetika pro FFT algoritmus (odmocnina, logaritmus)
  5. "macros.inc" - hromada základních assemblerovských maker
  6. "FFT.c" - definice globálního pracovního pole FFTwarr[], ukázkové funkce
  7. "FFT.h" - společný hlavičkový soubor pro celou FFT implementaci

Zbytek je součást ukázkového programu.

Zdrojáky ke stažení: AVR_FFT_DIT_r2.zip (108kB).

3.2.1 Modul "FFT_routines.s"

   Jde o hlavní modul celé FFT implementace. Jsou zde funkce: 

void FFT_input(void);

provádějící okéknování a bitovou reverzi adres, dále: 

void FFT_dit_r2(void);

provádějící vlatní FFT transformaci a na konec: 

void FFT_out_lin(void);
void FFT_out_log(void);

které vypočtou amplitudové spektrum, případně navíc provedou logaritmování s normalizací na 0dB. Všechny funkce pracují se společným globálním polem komplexních prvků: 

int16_t FFTwarr[FFTN*2];

Komplexní čísla jsou v poli uložena postupně po složkách, tj. re{0}, im{0}, re{1}, im{1}, ..., re{FFTN-1}, im{FFTN-1}. Použití FFT knihovny je zhruba následující:

  1. Naplnit IMAGINÁRNÍ prvky pole FFTwarr[] reálnou zdrojovou řadou dat o délce FFTN. Data musí být v 16-bit znaménkovém tvaru. Reálnou složku není třeba nulovat, bude přepsána funkcí FFT_input().

  2. Zavolat funkci FFT_input(), která provede bitovou inverzi adres a aplikuje na data okno (pokud tedy není vybráno obdélníkové), výsledek uloží do reálných prvků pole a původní imaginární prvky buďto vynuluje nebo do nich zduplikuje reálnou složku (nastavení FFTdupim).

  3. Zavolat funkci FFT_dit_r2(), která provede vlastní FFT transformaci. Vše probíhá na místě, takže po skončení této rutiny obsahuje pole FFTwarr[] komplexní spektrum (už s prvky ve správném pořadí).

  4. V případě potřeby zavolat funkci FFT_out_lin(), která z komplexního spektra vytvoří lineární amplitudové spektrum. Výsledné spektrum je uloženo zpět do pole FFTwarr[], ale tentokrát už ne na sudé adresy (do re{}), ale postupně, tj. od prvku 0, do FFTN/2-1 (je vypočtena pouze polovina spektra - druhá polovina je identická). Pro fullscale vstupní signál, obdélníkové okno a FFTdupim=1 se amplitudy spektra pohybují od 0 do 32768, při použití jiných oken jsou adekvátně nižší, viz. teorie.

  5. Eventuleně MÍSTO FFT_out_lin() zavolat FFT_out_log(), která provede sice totéž, ale v logaritmickém měřítku. Tato rutina vrací znaménkové výsleky přímo v dB ve fixed point formátu (fx 8.8). Logaritmování je zde realizováno rutinkou FFT_log10f_asm z modulu FFT_math.s. Tato rutinka převede lineární amplitudou do logaritmického měřítka s normalizací na y=0dB pro fullscale sinus a FFTdupim=1. Funkce je vybavena lookup tabulkami pro všechna okna, takže by měla vždy dávat správné výsledky.

   Pokud jde o možnosti nastavení algoritmu, tak byl proti původní implementaci přidán jen jedem parametr navíc a sice FFTdupim. Seznam a význam jednotlivých nastavení uvádí následující tabulka:

Parametr Význam
FFTN Velikost transformace od 32 do 512, po doplnění lookup tabulek i menší.
FFTW Použité okno (wHANN-Hann, wHAMM-Hamming, wBLAC-Blackman, wFLAT-Flattop, wRECT-obdélník).
FFTdupim Duplikuje vstupní signál do imaginární složky (zvýšení amplitudy signálu o 3dB). Výstupní spektrum bude sice fázově posunuto, ale zvýší se odstup signál/šum algoritmu.
FFTprec Zapne jisté numerické korekce, které citelně sníží šum algoritmu, ale za cenu o cca 12% nížího výkonu.
FFTopt Zapne zjednodušování motýlku pro úhly twiddle faktoru 0 a 90°, nárůst výkonu za cenu delšího kódu (patrné zejména pro malé FFTN).
FFTfsqrt Nahradí přesnou rutinu 32-bit odmocniny od ChanN méně přesnou lookup verzí, která je však násobně rychlejší (a také větší).

   K tomuto modulu navíc přímo patří lookup tabulky "FFT_lookup.inc", vyšší makra "FFT_macros.inc" a základní makra "macros.inc" (společná pro všechny assemblerovské soubory).

3.2.2 Modul "FFT_tables.inc"

   Zde jsou umístěny všechny lookup tabulky FFT algoritmu. Jednak je zde tabulka pro bitovou reverzi adres TFFTbrv, dále předpočítaný sin() a cos() (TFFTsico) v rozsahu 0 až 180° a na konec tabulky oken TFFTwdw. U znaménkových oken (např. Flattop) musí být navíc definováno: 

	.equ FFTWS,1

   Tabulky jsem předgeneroval jen pro rozsah 32 až 512 bodů, pro větší není implementace stavěná, menší lze vygenerovat pomocí malé utilitky: AVR_FFT_lookup.zip (64kB)

3.2.3 Modul "FFT_math.s"

   Tento modul obsahuje aritmetiku použitou FFT algoritmem. Předně je zde rutinka 32-bit odmocniny od ChanN FFT_sqrt32c_asm (není přímo volatelná jako C funkce) a její GCC wrapper: 

uint16_t FFT_sqrt32c(uint32_t x);

který již přímo volatelný z C části programu je. Takto odděleně je funkce řešena z toho důvodu, aby dobře "sedla" do vlastního FFT algoritmu bez zbytečné omáčky (záloha registrů), kterou vyžaduje GCC. Další funkcí je rychlá 32-bit odmocnina FFT_sqrt32f_asm a její GCC wrapper: 

uint16_t FFT_sqrt32f(uint32_t x);

Tato funkce je řešena pomocí dvojice lookup tabulek s interpolací a je velmi rychlá, nicméně vyžaduje dost FLASH pro tabulky a její přesnost je omezená na asi 0.6% (většina rozsahu x má chybu mnohem nižší).
   Na konec je zde rutinka provádějící převod lineární amplitudy do logaritmického měřítka FFT_log10f_asm a opět její GCC kompatibilní wrapper: 

int16_t FFT_log10f(uint16_t x);

Funkce je řešena pomocí trojice lookup tabulek a lineární interpolace. Obsahuje sadu lookup tabulek pro každé okno, takže je zajištěno, že fullscale sinu odpovídá vždy výstup y=0dB. Rozsah výstupu je podle okna od cca -88dB do +6dB. Všechno mimo je ořezáno na tento rozsah. Výstupní formát je ve tvaru fixed point (fx 8.8). Pokud by bylo třeba generovat lookup pro jiná okna případně jiná rozlišení, pak je k disopzici utilitka pro jejich generování log10lookup.zip (64kB).
   Prototypy všech těchto funkcí jsou ve společném hlavičkovém souboru "FFT.h".

3.2.4 Modul "main.c"

   Zde je jednoduchá demonstrační apliakce. Ukázkový prográmek je navržen pro jendočip ATmega644, který má poměrně dost RAM (4kB), takže lze bez obtíží implementovat i 512-ti bodové FFT. Komunikace s PC je opět řešena přes virtuální USB-COM port na 2Mbd bez řízení toku, ale lze použít i klasický COM port na 115200bd, nicméně odezva bude dost pomalá.
   Jsou realizovány celkem tři příkazy. Jednak samotný výpočet FFT s měřením počtu cyklů (příkaz 'F'), dále testovací smyčka pro algoritmus odmocniny sqrt32f() (příkaz 'S') a nakonec testovací smyčka pro oveřování algoritmu pro logaritmování amplitudového spektra log10f() (příkaz 'L').

   Příkaz 'F':

  1. PC vyšle 'F'.
  2. MCU odpoví 'A'.
  3. PC pošle byte s požadavkem (bit0: 0-pouze aplikace okna, 1-kompletní FFT, bit1: 0-linární spektrum, 1-logaritmické spektrum).
  4. MCU odešle word s velikostí transformace FFTN.
  5. MCU odešle dword s frekvencí hodin.
  6. MCU odešle kód okna (0-Hann, 1-Hamming, 2-Blackman, 3-Flattop, 4-Obdélník).
  7. PC odešle signál k transformaci (FFTN znaménkových wordů).
  8. MCU provede výpočet a odešle 'D'.
  9. MCU odešle změřené počty cyklů (v F_CPU/8):
    1. word pro FFT_out_lin() nebo FFT_out_log().
    2. word pro FFT_dit_t2().
    3. word pro FFT_input().
  10. MCU odešle transformovaná data. Reálnou složku časového průběhu nebo první polovinu amplitudového spektra (v obou případech FFTN/2 wordů).

   Příkaz 'S':

  1. PC vyšle 'S'.
  2. MCU odpoví 'A'.
  3. PC pošle word s požadovaným počtem testů N.
  4. PC pošle dword k odmocnění x.
  5. MCU pošle word y=FFT_sqrt32c(x) (přesná odmocnina).
  6. MCU pošle word y=FFT_sqrt32f(x) (rychlá odmocnina).
  7. Opakovat N-krát od bodu 4).

   Příkaz 'L':

  1. PC vyšle 'L'.
  2. MCU odpoví 'A'.
  3. PC pošle word s požadovaným počtem testů N.
  4. PC pošle word s amplitudou x.
  5. MCU pošle znaménkový word y=FFT_log10f(x).
  6. Opakovat N-krát od bodu 4).

   Na ostatní příkazy reaguje MCU chybovým znakem 'E'.


(c) 2010-2012, Stanislav Mašláň

Poslední aktualizace: 28.2.2012 Up