
Po úpěšné implementaci Cooley-Tukey FFT algoritmu na AVR, která se ukázala být ještě o něco výkonnější, než AVRFFT z webu www.elm-chan.org, kterou jsem se inspiroval, jsem si řekl, že by nebylo od věci zkusit nějakou pokročilejší optimalizační metodu výpočtu spektra. Vzhledem k mým dřívějším experimentům s transformacemi v rámci jednoho VŠ předmětu o zpracování dat jsem se rozhodl pro Hartleyovu transformaci. Ta se mi zdála na první pohled celkem jednoduchá a výhodná pro jednočipy, protože nepracuje s komplexními čísly, ale pouze s reálným pracovním polem. Tak lze ušetřit polovinu RAM a navíc zvýšit rychlost výpočtu. Výstup transformace se však dá velmi jednoduše přepočítat na komplexní spektrum odpovídající DFT, pokdu by bylo třeba.
Diskrétní Hartleyova transformace (DHT) je definována velmi jednoduchým vztahem:
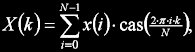
kde N je velikost transformace a funkce cas() je definována jako:
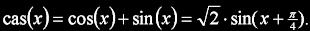
Proti DFT jsou tedy bázové funkce jednoduší a při přímé implementaci by stačilo N2 obyčejných součinů (proti 4*N2 součinů u DFT).
Vztah DHT transformace k DFT je jednoduchý, jedná se o rozdíl reálné a imaginární složky DFT spektra:
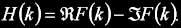
Ze jejich vztahu a vlastností DFT je také zřejmé, že lze DHT zpětně přepočítat na DFT:
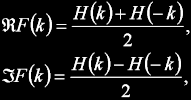
kde pro záporné indexování platí:
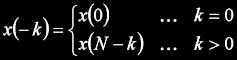
Amplitudové spektrum lze u DHT vypočítat následovně:
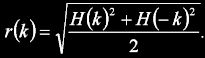
Jeho výpočet tedy zjevně není o nic složitější, než pro DFT, takže lze předpokládat, že DHT musí mít při výpočtu amplitudového spektra vyšší výkon.
DHT sama o sobě je pro výpočet spektra efektivnější, než DFT, nicméně podobně jako DFT má jisté příznivé vlastnosti, které umožňují
její zefektivnění. Celkové odvození je pěkně popsáno např. v [1] nebo [2].
Optimalizace je založena na stejném principu, jako u FFT, tj. na půlení zdrojové řady a dopočítávání druhé poloviny spektra.
Prvním krokem je rozdělit vstupní posloupnost na sudé a liché prvky:
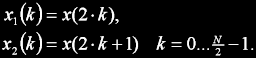
Řada x1 zůstala proti originálu x neposunutá, ale x2 tvořená lichými prvky již časově posuntá je,
takže stejně jako u DFT bude třeba provést při skládání dílčích DHT adekvátní posuv v obraze.
To bylo u DFT snadné, protože šlo o pouhé natočení vektorů spektra násobením exponenciálou (twiddle faktor), viz
popis FFT,
ale pro DHT je situace poněkud složitější, protože posuv ve spektru je definován jako:
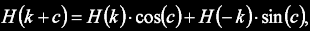
kde c je velikost posuvu. Výsledná DHT vypočtená z dílčích řad x1 a x2 pak bude vypadat takto:
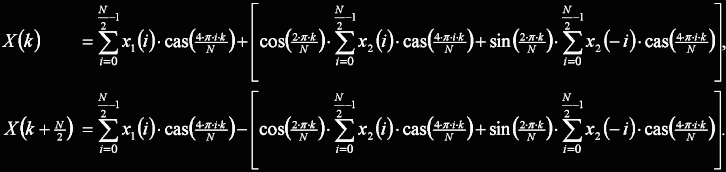
Jak je vidět, tak proti DFT je situace složitější. Původní DHT délky N se rozpadla na tři DHT délky N/2. Celkem nepříjemnou skutečností
komplikující realizaci je fakt, že jedna z nich je navíc počítána z převrácené řady x2(-k), ale i tak bude implementace efektivnější, než u FFT.
Pokud měla zdrojová řada velikost N=2M, pak lze půlit dále, až zůstane DHT řádu N=4, kterou lze zapsat jako:
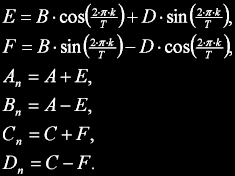
kde A, B, C a D jsou vstupy a výstupy DHT, k/T je úhel rotace. Je zde nápadná podobnost s DFT motýlkem.
V zásadě se jedná o kombinaci dvou DFT motýlků se společným twiddle faktorem, jen se nepočítá s komplexními vstupy, ale se dvěma páry vstupních prvků tvořící pomyslné komplexní číslo (vektor).
Způsobů, jak tento algoritmus zakreslit graficky, je jistě celá řada, ale mě se vzhledem k přehlednosti docela osvědčil tento:
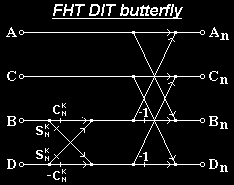 |
kde pro koeficienty SNk a CNk platí:
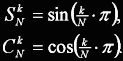
Stejně jako u FFT se zde nabízí možnost tyto koeficienty pro příznivé úhly vynechat. Příklad DHT algoritmu již s touto optimalizací pro velikost N=16
ukazuje následující diagram:
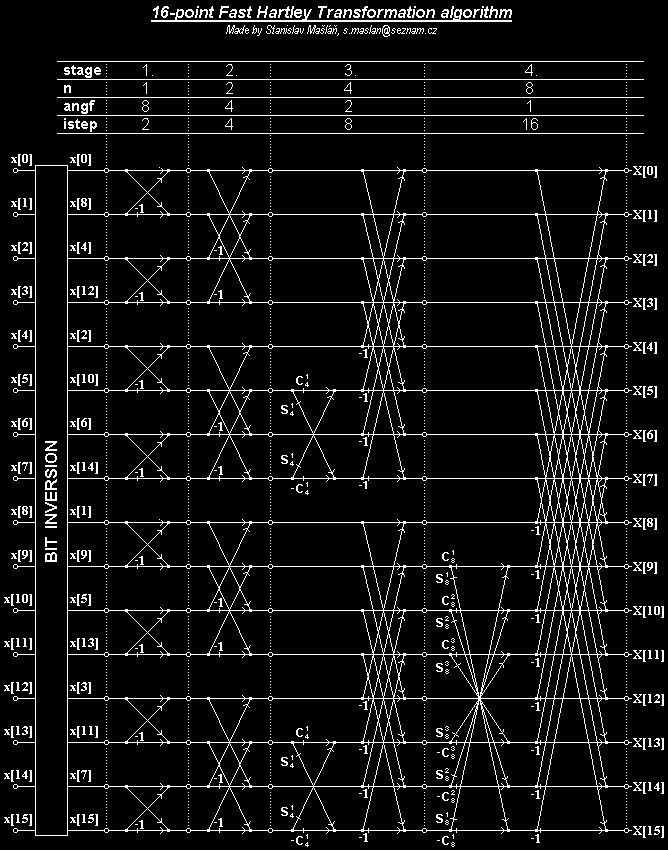 |
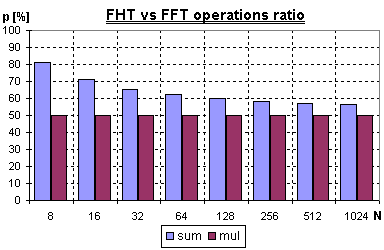
Díky optimalizacím jsou první etapy složené jen z DFT motýlků bez rotace (násobení twiddle faktorem) a dále odpadají násobení pro S,CN0 a S,CNn. V zájmu redukce velikosti lookup tabulek pro sin() a cos() je zde využito jejich periodicity, takže index k pro k>n/2 je nahrazen indexem n-k. Proto se také vyskytuje u spodního cosinu záporné znaménko. Celkový počet operací takto zjednodušeného algoritmu je celkem obtížně na vyjádřitelný vztahem, takže uvádím pouze tabulku s příklady pro konkrétní N, pro FHT a obdobně optimalizované FFT:
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||
Počet násobení klesl na polovinu a součtů cca na 60% pro N=256. Co do počtu operací, bude FHT téměř dvakrát rychlejší, než FFT, ale v reálu
něco výkonu navíc sebere složitější indexování dat.
Výše uvedené platí pro variantu decimace v čase (DIT).
Postup pro decimaci ve frekvenci naznačuje [3].
Zdroj [1] mimo odvození uvádí také konkrétní implementaci v jazyce Ratfor (Rational Fortran), která se zdá být celkem efektivní, jen nevyužívá pointery, takže jsem ji trochu upravil pro své potřeby. Možný příklad implementace v C v přesnosti double ukazuje následující kód:
#define N 16
// sin(k/N*pi), cos(k/N*pi), ... (k=0..N/2-1)
double tsincos[N]={0.000, 1.000, 0.3827, 0.9239, ...};
double FHTwarr[N];
void FHT(void)
{
int n=1;
int angf=N/2;
while(n<N)
{
double *ang=&tsincos[0];
double *A=&FHTwarr[0];
double *B=&FHTwarr[n];
double *C=&FHTwarr[n-1];
double *D=&FHTwarr[n*2-1];
// ang=0
for(k=0;k<angf;k++)
{
double tmp=*B;
*B=*A-tmp;
*A=*A+tmp;
A+=n<<1;
B+=n<<1;
}
A-=(N-1);
B-=(N-1);
// full butterflies
while(n>2 && ang<n)
{
ang+=angf<<1;
dsin=ang[0];
dcos=ang[1];
for(k=0;k<angf;k++)
{
double E=*B*dcos + *D*dsin;
double F=*B*dsin - *D*dcos;
*B=*A-E;
*A=*A+E;
*D=*C-F;
*C=*C+F;
A+=n<<1;
B+=n<<1;
C+=n<<1;
D+=n<<1;
}
A-=(N-1);
B-=(N-1);
C-=(N+1);
D-=(N+1);
}
// ang=pi/2
for(k=0;n>1 && k<angf;k++)
{
double tmp=*D;
*D=*C-tmp;
*C=*C+tmp;
C+=n<<1;
D+=n<<1;
}
n<<=1;
angf>>=1;
}
}
Algoritmus pracuje s již přeskládanými daty (je třeba nejdříve provést bitovou inverzi adres)!
Sinus a cosinus je opět předpočten a to pouze v rozashu 0 až 90° (polovina proti FFT). Vlastní výpočet je
dělen na tři části. První odpovídá úhlu 0°, takže byla zjednodušena na prosté součty/rozdíly. Stejné zjednodušení je provedeno
pro úhel 90° (uplatňuje se až od druhé etapy). Plný dvojitý motýlek se provádí až od třetí etapy a to jen pro úhly mimo 0 a 90°.
Jak je vidět, tak pro rozumně efektivní implementaci je potřeba ideálně pět pointerů, což trochu komplikuje situaci nejen na 8-bit AVR.
Holt se to tentokrát neobejde bez nějakých těch proměnných v RAM, ale vzhledem k délce výpočtu vektorové rotace (přes 80 cyklů pro AVR) se to snad ztratí.
V popisu k FFT jsem se nijak nezmínil o jedné docela podstatné operaci, kterou je třeba provádět při výpočtu ve fixed point (integer). Pokud mají mezivýsledky v jednotlivých etapách zůstat v mezích integeru, je třeba provádět průběžně měřítkování. Tímto tématem se detailně zabývá nejeden článek, nicméně většinou se použije prosté dělení dvěma. Nejlépe lze operaci pochopit na příkladu, takže uvádím příklad 16-bit implementace:
#define N 16
// sin(k/N*pi), cos(k/N*pi), ... (k=0..N/2-1) [fx 1.15]
int16 tsincos[N]={0, 32767, 12540, 30273, ...};
int16 FHTwarr[N];
void FHT(void)
{
int16 n=1;
int16 angf=N/2;
while(n<N)
{
int16 *ang=&tsincos[0];
int16 *A=&FHTwarr[0];
int16 *B=&FHTwarr[n];
int16 *C=&FHTwarr[n-1];
int16 *D=&FHTwarr[n*2-1];
// ang=0
for(k=0;k<angf;k++)
{
int16 b=*B/2;
int16 a=*A/2;
*A=a+b;
*B=a-b;
A+=n<<1;
B+=n<<1;
}
A-=(N-1);
B-=(N-1);
// full butterflies
while(n>2 && ang<n)
{
ang+=angf<<1;
dsin=*ang[0];
dcos=*ang[1];
for(k=0;k<angf;k++)
{
E=(int16)((int32)*B*dcos + (int32)*D*dsin)/65536;
F=(int16)((int32)*B*dsin - (int32)*D*dcos)/65536;
int16 a=*A/2;
int16 C=*C/2;
*A=a+E;
*B=a-E;
*C=c+F;
*D=c-F;
A+=n<<1;
B+=n<<1;
C+=n<<1;
D+=n<<1;
}
A-=(N-1);
B-=(N-1);
C-=(N+1);
D-=(N+1);
}
// ang=pi/2
for(k=0;n>1 && k<angf;k++)
{
int16 c=*C/2;
int16 d=*D/2;
*C=c+d;
*D=c-d;
C+=n<<1;
D+=n<<1;
}
n<<=1;
angf>>=1;
}
}
Pro zvýšení odstupu signál/šum je navíc možné doplnit zaokrouhlování, ale to se na úrovni C děla špatně, takže není součástí kódu. Alternativně by také bylo možné dočasně počítat ve vyšší přesnosti, protože při operaci (a/2+b/2) oproti (a+b)/2 dojde k chybám. Pro mírný nárůst výkonu lze nahradit dělení rotacemi vpravo, ale samozřejmě se to podepíše na přesnosti, protože aritmetická rotace vpravo není symetrická kolem nuly. Takto vniklé chyby porostou s každou další etapou algoritmu. Chytrý překldač však převede dělení dvěma na rotaci s korekcí, takže nároky nebudou nijak drastické, ale např. zrovna AVRGCC se s tím nezatěžoval a práskl mi tam 16/16-bit dělení. :-) Holt nic není dokonalé.
Zde je pár docela dobrých zdrojů nejen ohledně Hartleyovy transformace.
| [1] | ULLMANN, Ronald. An algorithm for the Fast Hartley Transform. Stanford Exploration Project Volume 36 Issue 2, 1987. Dostupné z www: http://sepwww.stanford.edu/theses/sep38/38_29.pdf |
| [2] | REEVES, Arlo. Optimized Fast Hartley Transform for the MC68000 with applications in image processing. Thayler School of Engineering, Dartmouth Collage, Hanover, New Hampshire. March 1990. Dostupné z www: http://imagej.nih.gov/ij/download/docs/ImageFFT/thesis.pdf |
| [3] | WEISSTEIN, ERIC W. Hartley Transform. MathWorld. Dostupné z www: http://mathworld.wolfram.com/HartleyTransform.html |
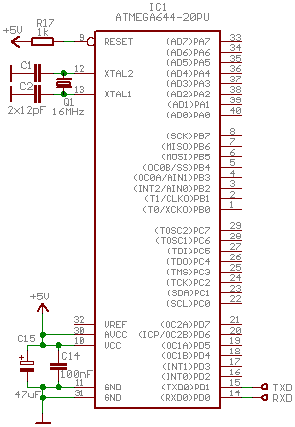
Zapojení je identické se zapojením pro testování FFT implementace. Opět se jedná o ATmega644 na 16MHz, komunikace přes USART na 2Mbd, bez parity a řízení toku. Pokud nevadí dlouhá odezva, pak lze zpomalit na takty vhodné pro COM port.
 |
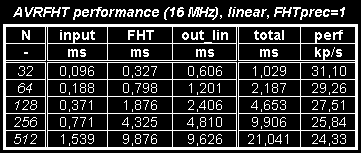
Po odladění jsem provedl nějaká ta měření výkonu. Dle očekávání šlape algoritmus podstatně rychleji. Výsledky jsou uvedeny v následujících tabulkách:
|
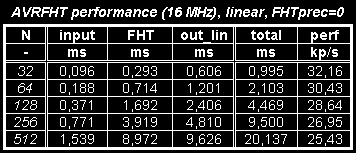
|

|

|
Pro FHT už více času zabere výpočet amplitudového spektra, než vlastní FHT algoritmus. Výkon by se dal dost zvýšit použitím interpolované odmocniny, ale pro objektivní srovnání s FFT implementací jsem použil přesnou 32-bit odmocninu. Pro srovnání s FFT jsem zvolil nastavení FFTopt=1, FFTprec=1 a lineární spektrum, což asi nejvíce odpovídá použitým optimalizacím u FHT:
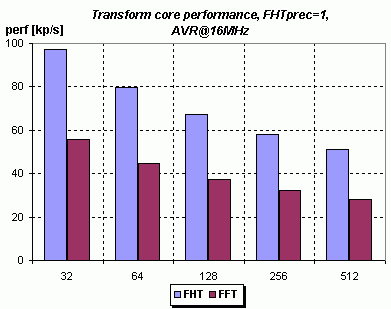
|
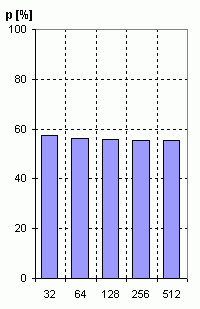
|
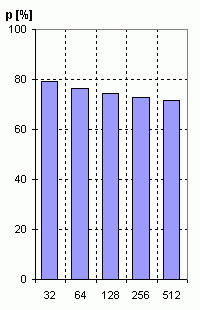
Samotná transformace je i přes komplikace s nedostatkem pracovních registrů a složitějším přstupem k RAM téměř dvakrát rychlejší, ale celkový výkon dost sráží zmněný výpočet amplitudového spektra (32-bit odmocnina):
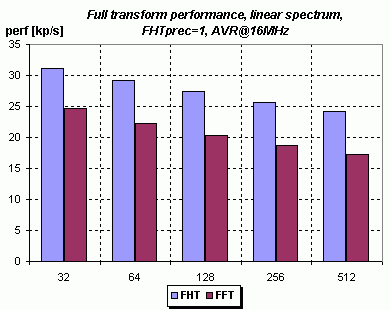
|
|
Výkon v tomto případě vzrostl proti původní FFT asi na 140% pro N=256.
Pro spektrum v logaritmickém měřítku se zpomalení výpočtem spektra až tak neprojeví, protože jsem ho vyřešil přes lookup
tabulky s interpolací (cca 4x rychleší, než 32-bit odmocnina). Zde je nárůst výkonu asi na 160% pro N=256.
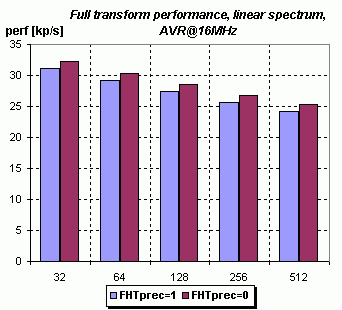
Všechny grafy jsou vytvořeny pro vyšší přesnost výpočtu FHTprec=1. Rychlejší a méně přesná varianta
je maximálně asi o 12% pomalejší, ale rozdíl se opět dost stírá výpočtem amplitudového spektra (pod 5% pro lineární spektrum):
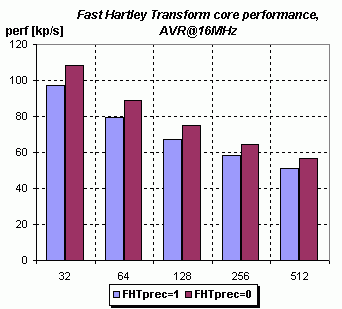
|
|
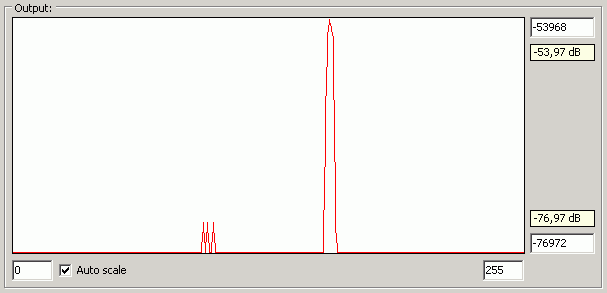
Komunikace by měla být kompatibilní s programem pro testování FFT implementace. V souboru "config.ini" stačí nastavit číslo portu a baudrate a mělo by to chodit.
|
|
Program ke stažení: AVR_FFT_tester_v3.zip (365kB).
K vlastní implementaci AVR FFT patří pouze následující soubory:
- "FHT_routines.s" - vlastní rutinky FHT transformace
- "FHT_macros.inc" - vyšší makra pro FHT algoritmus
- "FHT_tables.inc" - lookup tabulky FHT algoritmu
- "FHT_math.s" - rychlá aritmetika pro FHT algoritmus (odmocnina, logaritmus)
- "macros.inc" - hromada základních assemblerovských maker
- "FHT.c" - globální pracovní pole FHTwarr[], ukázkové funkce
- "FHT.h" - společný hlavičkový soubor pro celou FHT implementaci
Zbytek je součást ukázkového programu.
Zdrojáky ke stažení (11.4.2014): AVR_FHT.zip (54kB).
Zdrojáky ke stažení (1.4.2012): AVR_FHT_2012_04_01.zip (54kB).
Jde o hlavní modul celé FHT implementace. Jsou zde funkce:
void FHT_input(int16_t *src);
provádějící okéknování a bitovou reverzi adres ze zdrojových dat src. Na rozdíl od původní FFT implementace musí být zdrojová data jinde, než v globálním pracovním poli FHTwarr[]! Pokud jsou vzorky pro zpracování získávány průběžně např. z ADC, tak lze adaptovat a použít C funkci z modulu "FHT.c" provádějící totéž. Dále je zde funkce:
void FHT_do(void);
provádějící vlastní FHT transformaci a na konec:
void FHT_out_lin(void); void FHT_out_log(void);
které vypočtou amplitudové spektrum, případně navíc provedou logaritmování s normalizací na 0dB. Všechny funkce pracují se společným globálním polem:
int16_t FHTwarr[FHTN];
Použití FHT knihovny je zhruba následující:
Zavolat funkci FHT_input(data), která provede bitovou inverzi adres a okénkování reálných vstupních dat data a uloží výstup do pracovního pole FHTwarr[].
Zavolat funkci FHT_do(), která provede vlastní FHT transformaci. Vše probíhá na místě, takže po skončení této rutiny obsahuje pole FHTwarr[] obraz s prvky ve správném pořadí.
V případě potřeby zavolat funkci FHT_out_lin(), která z FHT spektra vytvoří lineární amplitudové spektrum. Výsledné spektrum je uloženo zpět do pole FHTwarr[], (je vypočtena pouze polovina spektra - druhá polovina je identická). Pro fullscale vstupní signál a obdélníkové okno se amplitudy spektra pohybují od 0 do 32768, při použití jiných oken jsou adekvátně nižší.
Eventuelně MÍSTO FHT_out_lin() zavolat FHT_out_log(), která provede sice totéž, ale v logaritmickém měřítku. Tato rutina vrací znaménkové výsleky přímo v dB ve fixed point formátu (fx 8.8). Logaritmování je zde realizováno rutinkou FFT_s32log10f_asm z modulu FHT_math.s. Tato rutinka slučuje odmocninu i logaritmování s normalizací na y=0dB pro fullscale sinus. Funkce je vybavena lookup tabulkami pro všechna okna, takže by měla vždy dávat správné výsledky.
Pokud jde o možnosti nastavení algoritmu, tak jsou značně menší, něž pro FFT:
| Parametr | Význam |
|---|---|
| FHTN | Velikost transformace od 32 do 512, po doplnění lookup tabulek i menší. |
| FHTW | Použité okno: wHANN-Hann, wHAMM-Hamming, wBLAC-Blackman, wFLAT-Flattop, wRECT-obdélník. |
| FHTfsqrt | Nahradí přesnou rutinu 32-bit odmocniny od ChanN méně přesnou lookup verzí, která je však násobně rychlejší (a také větší). |
K tomuto modulu navíc přímo patří lookup tabulky "FHT_lookup.inc", vyšší makra "FHT_macros.inc" a základní makra "macros.inc" (společná pro všechny assemblerovské soubory).
Zde jsou umístěny všechny lookup tabulky FHT algoritmu. Jednak je zde tabulka pro bitovou reverzi adres TFHTbrv, kde jsou cílové relativní adresy udané v bytech. Dále je zde předpočítaný sin() a cos() (TFHTsico) v rozsahu 0 až 90° normalizovaný na amplitudu 32768 místo 32767 protože zde funkce nabývá jen kladních hodnot. Na konec jsou zde tabulky oken TFHTwdw. U znaménkových oken (např. Flattop) musí být navíc definováno:
.equ FHTWS,1
Tabulky jsem předgeneroval jen pro rozsah 32 až 512 bodů, pro větší není implementace stavěná, menší lze vygenerovat pomocí utilitky: AVR_FFT_lookup.zip (67kB)
Tento modul obsahuje aritmetiku použitelnou FFT/FHT algoritmem. Předně je zde rutinka 32-bit odmocniny od ChanN FFT_sqrt32c_asm (není přímo volatelná jako GCC funkce) a její GCC wrapper:
uint16_t FFT_sqrt32c(uint32_t x);
který již přímo volatelný z C části programu je. Takto odděleně je funkce řešena z toho důvodu, aby dobře "sedla" do vlastního FHT algoritmu bez zbytečné omáčky (zálohy registrů), kterou vyžaduje GCC. Další funkcí je rychlá 32-bit odmocnina FFT_sqrt32f_asm a její GCC wrapper:
uint16_t FFT_sqrt32f(uint32_t x);
Tato funkce je řešena pomocí dvojice lookup tabulek s interpolací a je velmi rychlá,
nicméně vyžaduje dost FLASH pro tabulky a její přesnost je omezená na asi 0.6%
(většina rozsahu x má chybu mnohem nižší).
Na konec je zde rutinka FFT_s32log10f_asm a opět
její GCC kompatibilní wrapper:
int16_t FFT_s32log10f(uint32_t x);
Tato funkce slučuje výpočet 32-bit odmocniny s logaritmováním do jedné funkce, což je změna
proti verzi použité u FFT. Provádí následující výpočet:
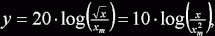
kde xm je hodnota x pro kterou bude vráceno 0dB. Funkce vrací amplitudu přímo v dB
ve znaménkovém formátu fixed point 8.8-bit. Je realizována pomocí trojice lookup tabulek s různým krokem s lineární intepolací.
Jsou zde tabulky pro všechna okna, takže amplituda pro fullscale sinus by měla být vždy 0dB.
Na generátoru lookup tabulke jsem si tentokrát dal hodně záležet, takže je
přesnost funkce celkem uspokojivá. V celém rozsahu chyba nepřesahuje ±3 LSB (cca ±0.012dB). Rozložení chyb ukazuje následující histogram:
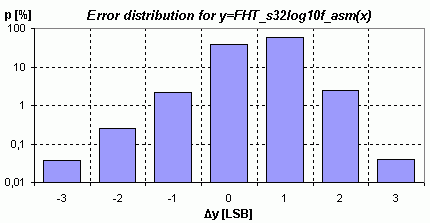
|
Pokud by bylo třeba generovat lookup pro jiná okna (jiné xm), pak je k disopzici
utilitka pro jejich generování: sqrt32log10f_lookup.zip (64kB).
Prototypy všech těchto funkcí jsou ve společném hlavičkovém souboru "FHT.h".
Zde je jednoduchá demonstrační aplikace zcela kompatibilní s FFT implementací. Jsou realizovány celkem tři příkazy. Jednak samotný výpočet FFT s měřením počtu cyklů (příkaz 'F'), dále testovací smyčka pro algoritmus odmocniny sqrt32f() (příkaz 'S') a nakonec testovací smyčka pro oveřování algoritmu pro logaritmování amplitudového spektra log10f() (příkaz 'L').
Příkaz 'F':
- PC vyšle 'F'.
- MCU odpoví 'A'.
- PC pošle byte s požadavkem (bit0: 0-pouze aplikace okna, 1-kompletní FHT, bit1: 0-linární spektrum, 1-logaritmické spektrum).
- MCU odešle word s velikostí transformace FHTN.
- MCU odešle dword s frekvencí hodin.
- MCU odešle kód okna (0-Hann, 1-Hamming, 2-Blackman, 3-Flattop, 4-Obdélník).
- PC odešle signál k transformaci (FHTN znaménkových wordů).
- MCU provede výpočet a odešle 'D'.
- MCU odešle změřené počty cyklů (v F_CPU/8):
- word pro FHT_out_lin() nebo FHT_out_log().
- word pro FHT_do().
- word pro FHT_input().
- MCU odešle transformovaná data. Časový průběh nebo amplitudové spektrum (v obou případech FHTN wordů).
Příkaz 'S':
- PC vyšle 'S'.
- MCU odpoví 'A'.
- PC pošle word s požadovaným počtem testů N.
- PC pošle dword k odmocnění x.
- MCU pošle word y=FHT_sqrt32c(x) (přesná odmocnina).
- MCU pošle word y=FHT_sqrt32f(x) (rychlá odmocnina).
- Opakovat N-krát od bodu 4).
Příkaz 'L':
- PC vyšle 'L'.
- MCU odpoví 'A'.
- PC pošle word s požadovaným počtem testů N.
- PC pošle word s amplitudou x.
- MCU pošle znaménkový word y=FHT_log10f(x).
- Opakovat N-krát od bodu 4).
Na ostatní příkazy reaguje MCU chybovým znakem 'E'.
| Poslední aktualizace: 1.4.2012 |  |
 |